.ipynb .pdf

repository open issue suggest edit

Binder

Contents

Collective Communications

Collective Communications A collective communication is a communication that involves a group (or groups) of processes.

• the group of processes is represented as always as a communicator that provides a context for the operation,

• Syntax and semantics of the collective operations are consistent with the syntax and semantics of the point-to-point operations,

• For collective operations, the amount of data sent must exactly match the amount of data specified by the receiver.

Mixing type of calls Collective communication calls may use the same communicators as point-to-point communication; Any (conforming) implementation of MPI messages guarantees that calls generated on behalf of collective communication calls will not be confused with messages generated by point-to-point communication.

Broadcast, Gather and Scatter

• The broadcast operation. In the broadcast, initially just the first process contains the data \(a_0\), but after the broadcast all processes contain it.

  

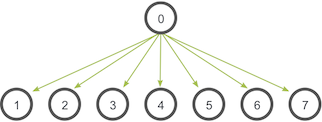
• This is an example of a one-to-all communication, i.e., only one process contributes to the result, while all processes receive the result.

int MPI_Bcast(void* buffer, int count, 
 MPI_Datatype datatype, int root, MPI_Comm comm)

Broadcasts a message from the process with rank root to all processes of the group, itself included.

• void* buffer on return, the content of root’s buffer is copied to all other processes.

• int count size of the message

• MPI_Datatype datatype type of the buffer

• int root rank of the process broadcasting the message

• MPI_Comm comm communicator grouping the processes involved in the broadcast operation

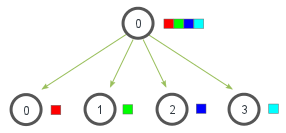
The scatter and gather operations

• In the scatter, initially just the first process contains the data \(a_0,\ldots,a_3\), but after the scatter the \(j\)th process contains the \(a_j\) data.

  

• In the gather, initially the \(j\)th process contains the \(a_j\) data, but after the gather the first process contains the data \(a_0,\ldots,a_3\)

  

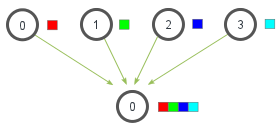
  Each process (root process included) sends the contents of its send buffer to the root process. The latter receives the messages and stores them in rank order.

  int MPI_Gather(const void* sendbuf, int sendcount, 
    MPI_Datatype sendtype,  void* recvbuf, int recvcount, 
    MPI_Datatype recvtype, int root, MPI_Comm comm)
  

  • const void* sendbuf starting address of send buffer

  • int sendcount number of elements in send buffer

  • MPI_Datatype sendtype data type of send buffer elements

  • void* recvbuf [address of receive buffer]{.alert}

  • int recvcount [number of elements for any single receive]{.alert} (and [not]{.ul} the total number of items!)

  • MPI_Datatype recvtype [data type of received buffer elements]{.alert}

  • int root rank of receiving process

  • MPI_Comm comm communicator

Observe that

• The type signature of sendcount, sendtype on each process must be equal to the type signature of recvcount, recvtype at all the processes.

• The amount of data sent must be equal to the amount of data received, pairwise between each process and the root.

Therefore, if we need to have a varying count of data from each process, we need to use instead

int MPI_Gatherv(const void* sendbuf, int sendcount, 
 MPI_Datatype sendtype, void* recvbuf, 
 const int recvcounts[], const int displs[], 
 MPI_Datatype recvtype, int root, MPI_Comm comm)

where

• const int recvcounts[] is an array (of length group size) containing the number of elements that are received from each process,

• const int displs[] is an array (of length group size). Entry i specifies the displacement relative to recvbuf at which to place the incoming data from process i.

If we need to have the result of the gather operation on every process involved in the communicator we can use the variant

int MPI_Allgather(const void* sendbuf, int sendcount,
 MPI_Datatype sendtype, void* recvbuf, int recvcount,
 MPI_Datatype recvtype, MPI_Comm comm)

• All processes in the communicator comm receive the result. The block of data sent from the \(j\)th process is received by every process and placed in the \(j\)th block of the buffer recvbuf.

• The type signature associated with sendcount, sendtype, at a process must be equal to the type signature associated with recvcount, recvtype at any other process.

This function has also the version for gathering messages with different sizes:

int MPI_Allgatherv(const void* sendbuf, int sendcount,
 MPI_Datatype sendtype, void* recvbuf, const int recvcounts[],
 const int displs[], MPI_Datatype recvtype, MPI_Comm comm)

and works in a way analogous to the MPI_Gatherv.

The scatter is simply the inverse operation of MPI_Gather

int MPI_Scatter(const void* sendbuf, int sendcount, 
  MPI_Datatype sendtype, void* recvbuf, int recvcount, 
  MPI_Datatype recvtype, int root, MPI_Comm comm)

• const void* sendbuf [address of send buffer]{.alert}

• int sendcount [number of elements sent to each process]{.alert}

• MPI_Datatype sendtype [type of send buffer elements]{.alert}

• void* recvbuf address of receive buffer

• int recvcount number of elements in receive buffer

• MPI_Datatype recvtype data type of receive buffer elements

• int root rank of sending process

• MPI_Comm comm communicator

Taxonomy of collective communications: Scatter Observe that

• The type signature of sendcount, sendtype on each process must be equal to the type signature of recvcount, recvtype at the root.

• The amount of data sent must be equal to the amount of data received, pairwise between each process and the root.

Therefore, if we need to have a varying count of data from each process, we need to use instead

int MPI_Scatterv(const void* sendbuf, const int sendcounts[],
 const int displs[], MPI_Datatype sendtype, void* recvbuf,
 int recvcount, MPI_Datatype recvtype, int root, MPI_Comm comm)

where

• const int sendcounts[] is an array (of length group size) containing the number of elements that are sent to each process,

• const int displs[] is an array (of length group size). Entry i specifies the displacement relative to recvbuf from which to take the outgoing data to process i.

Modifying the 1st derivative code

Modifying the 1st derivative code Let us perform the following modification to our first derivative code:

1. Taking from input the number of points to use in each interval,

2. Collecting the whole result on one process and print it on file.

For the first step we use the MPI_Bcast function,

if(mynode == 0){
 if(argc != 2){
  n = 20;
 }else{
  n = atoi(argv[1]);
 }
}
MPI_Bcast(&n,1,MPI_INT,
 0,MPI_COMM_WORLD);

• We read on rank \(0\) the number n from command line,

• Then we broadcast it with MPI_Bcast, pay attention to the fact that the broadcast operations happens on all the processes!

Modifying the 1st derivative code Then we gather all the derivatives from the various processes and collect them on process 0.

if(mynode == 0)
 globalderiv = (double *) 
   malloc(sizeof(double) 
   *(n*totalnodes));

MPI_Gather(fx,n,MPI_DOUBLE,
  globalderiv,n,MPI_DOUBLE,
  0,MPI_COMM_WORLD);

• we allocate on rank 0 the memory that is necessary to store the whole derivative array,

• then we use the to gather all the array fx (of double) inside the globalderiv array.

At last we print it out on file on rank 0

if(mynode == 0){
 FILE *fptr; fptr = fopen("derivative", "w");
 for(int i = 0; i < n*totalnodes; i++)
  fprintf(fptr,"%f %f\n",globala+i*dx,globalderiv[i]);
 fclose(fptr); free(globalderiv);}

All-to-All Scatter/Gather

All-to-All MPI_ALLTOALL is an extension of MPI_ALLGATHER to the case where each process sends distinct data to each of the receivers.

int MPI_Alltoall(const void* sendbuf, int sendcount,
 MPI_Datatype sendtype, void* recvbuf, int recvcount, 
 MPI_Datatype recvtype, MPI_Comm comm)

• The \(j\)th block sent from process \(i\) is received by process \(j\) and is placed in the \(i\)th block of recvbuf.

• The type signature for sendcount, sendtype, at a process must be equal to the type signature for recvcount, recvtype at any other process.

All-to-All different data size If we need to send data of different size between the processes

int MPI_Alltoallv(const void* sendbuf, const int sendcounts[],
 const int sdispls[], MPI_Datatype sendtype, void* recvbuf,
 const int recvcounts[], const int rdispls[],
 MPI_Datatype recvtype, MPI_Comm comm);

• const void* sendbuf starting address of send buffer

• const int sendcounts[] array specifying the number of elements to send to each rank

• const int sdispls[] entry \(j\) specifies the displacement (relative to sendbuf) from which to take the outgoing data destined for process \(j\)

• void* recvbuf array specifying the number of elements that can be received from each rank

• const int recvcounts[] integer array. Entry \(i\) specifies the displacement (relative to recvbuf) at which to place the incoming data from process \(i\)

• const int rdispls[] entry \(i\) specifies the displacement (relative to recvbuf) at which to place the incoming data from process \(i\)

Global reduce operation

The reduce operation The reduce operation for a given operator takes a data buffer from each of the processes in the communicator group and combines it according to operator rules.

int MPI_Reduce(const void* sendbuf, void* recvbuf, 
 int count, MPI_Datatype datatype, MPI_Op op, 
 int root, MPI_Comm comm);

• const void* sendbuf address of send buffer

• void* recvbuf address of receive buffer

• int count number of elements in send buffer

• MPI_Datatype datatype data type of elements of send buffer

• MPI_Op op reduce operation

• int root rank of root process

• MPI_Comm comm communicator

The reduce operation The value of MPI_Op op for the reduce operation can be taken from any of the following operators.

Constant	Operation	Constant	Operation
MPI_MAX	Maximum	MPI_MAXLOC	Max value and location
MPI_MIN	Minimum	MPI_MINLOC	Minimum value and location
MPI_SUM	Sum	MPI_LOR	Logical or
MPI_PROD	Product	MPI_BOR	Bit-wise or
MPI_LAND	Logical and	MPI_LXOR	Logical exclusive or
MPI_BAND	Bit-wise and	MPI_BXOR	Bit-wise exclusive or

Moreover, if a different operator is needed, it is possible to create it by means of the function

int MPI_Op_create(MPI_User_function* user_fn, int commute, 
MPI_Op* op)

In C the prototype for a MPI_User_function is

typedef void MPI_User_function(void* invec, void* inoutvec, 
    int *len, MPI_Datatype *datatype);

Global reduce operation – All-Reduce As for other collective operations we may want to have the result of the reduction available on every process in a group.

The routine for obtaining such result is

int MPI_Allreduce(const void* sendbuf, void* recvbuf, 
 int count, MPI_Datatype datatype, MPI_Op op, MPI_Comm comm)

• const void* sendbuf address of send buffer

• void* recvbuf address of receive buffer

• int count number of elements in send buffer

• MPI_Datatype datatype data type of elements of send buffer

• MPI_Op op reduce operation

• MPI_Comm comm communicator

This instruction behaves like a combination of a reduction and broadcast operation.

Global reduce operation – All-Reduce-Scatter This is another variant of the reduction operation in which the result is scattered to all processes in a group on return.

int MPI_Reduce_scatter_block(const void* sendbuf, 
 void* recvbuf, int recvcount, MPI_Datatype datatype, 
 MPI_Op op, MPI_Comm comm);

• The routine is called by all group members using the same arguments for recvcount, datatype, op and comm.

• The resulting vector is treated as n consecutive blocks of recvcount elements that are scattered to the processes of the group comm.

• The \(i\)th block is sent to process \(i\) and stored in the receive buffer defined by recvbuf, recvcount, and datatype.

Global reduce operation – All-Reduce-Scatter Of this function also a variant with variable block–size is available

int MPI_Reduce_scatter(const void* sendbuf, void* recvbuf,
const int recvcounts[], MPI_Datatype datatype, MPI_Op op,
MPI_Comm comm);

• This routine first performs a global element-wise reduction on vectors of \(\verb|count|=\sum_{i=0}^{n-1}\verb|recevcounts[i]|\) elements in the send buffers defined by sendbuf, count and datatype, using the operation op, where n is the size of the communicator.

• The routine is called by all group members using the same arguments for recvcounts, datatype, op and comm.

• The resulting vector is treated as n consecutive blocks where the number of elements of the \(i\)th block is recvcounts[i].

• The \(i\)th block is sent to process \(i\) and stored in the receive buffer defined by recvbuf, recvcounts[i] and datatype.

Some computations using collective communications

Computing Integrals

For an integrable function \(f : [a,b] \rightarrow \mathbb{R}\) the midpoint rule (sometimes rectangle rule) is given by $\(\int_{a}^{b}f(x) dx \approx I_1 = (b-a) f\left(\frac{a+b}{2}\right),\)$

This is a very crude approximation, to make it more accurate we may break up the interval \([a,b]\) into a number \(n\) of non-overlapping subintervals \([a_k,b_k]\) such that \([a,b] = \cup_k [a_k,b_k]\), $\(I_n = \sum_{k=0}^n(b_k-a_k) f\left(\frac{a_k+b_k}{2}\right)\)$

Computing integrals with parallel midpoint quadrature rule If we want to transform this computation in a parallel computation we can adopt the following sketch:

1. if (mynode == 0) get number of intervals for quadrature

2. broadcast number of intervals to all the processes

3. assign the non-overlapping intervals to the processes

4. sum function values in the center of each interval

5. reduce with operator sum the integral on process 0.

As a test function for the parallel integration routine we can use $\(f(x) = \frac{4}{1+x^2}; \qquad I = \int_{0}^{1} \frac{4}{1+x^2} dx = \pi.\)$ To evaluate the error we can use the value : double PI25DT = 3.141592653589793238462643;

h   = 1.0 / ((double) n*totalnodes);
sum = 0.0;
for (i = 1+mynode*n;
    i <= n*(mynode+1);
    i++){
 x = h * ((double)i - 0.5);
 sum += f(x);
}
mypi = h * sum;
MPI_Reduce(&mypi, &pi, 1, 
    MPI_DOUBLE, 
    MPI_SUM, 0, 
    MPI_COMM_WORLD);

• We assume that all the intervals have the same size, thus the scaling h   = 1.0 / (double) n,

• We compute all the value \(x\) that are in the local process and increment the local sum,

• in conclusion we perform an MPI_Reduce to sum together all the local sums.

You can then print out the obtained value of \(\pi\) and the error with respect to PI25DT as

if (mynode == 0){
 printf("pi is approximately %.16f, Error is %e\n",
    pi, fabs(pi - PI25DT));
}

Python version

We can implement the same algorithm using MPI4PY.

%%file quadrature.py
"""
Computing pi with parallel quadrature formula
"""
import numpy
from mpi4py import MPI
import sys

comm = MPI.COMM_WORLD
mynode = comm.Get_rank()
totalnodes = comm.Get_size()

def fun(x):
    return (4.0/(1.0 + x*x))

truepi = 3.141592653589793238462643
dest = 0
pi = numpy.zeros(1)

# Initialize value of n only if this is rank 0
# we are not checking the input, if the user does something that
# has no meaning we are going to fail badly!
if mynode == 0:
    if len(sys.argv) == 1:
        n = numpy.full(1, 20, dtype=int) # default value
    else:
        n = numpy.full(1,int(sys.argv[1]),dtype=int)
else:
    n = numpy.zeros(1, dtype=int)

# Broadcast n to all processes
comm.Bcast(n, root=0)

# Compute local integral
my_pi = numpy.zeros(1)
h = 1.0/(n*totalnodes)
for i in numpy.arange(1+mynode*n,n*(mynode+1)+1):
    x = h*(i - 0.5)
    my_pi = my_pi + fun(x)    
my_pi = h*my_pi

# Send partition back to root process:
comm.Reduce(my_pi, pi, MPI.SUM, dest)

# Only print the result in process 0
if mynode == 0:
    print('The Integral Sum =', pi[0]," The Error is ",numpy.abs(pi[0]-truepi))

Overwriting quadrature.py

That we can execute as usual by doing

!mpiexec -np 4 python quadrature.py 50

The Integral Sum = 3.141594736923127  The Error is  2.083333333846582e-06

Random number generation: Montecarlo type algorithms

Montecarlo methods are algorithms that rely on a procedure of repeated random sampling to obtain numerical results1.

A generic Montecarlo algorithm can be described by the following 4 steps

1. define a domain of possible samples

2. generate the samples from a probability distribution over such domain

3. perform a deterministic computation on the inputs

4. aggregate the results

We can write the parallel version of such algorithm in the following way

1. we divide a square in an number of parts equal to the number of processes we have,

2. we generate a number of random points \((x,y)\) in the area owned by each process,

3. we compute how many points fall in the circle

4. sum-reduce the number of points in the square and in the circle

5. divide the two numbers on process 0 to get the approximation

We can generate on each node the sampling on the reference square by

h  = 2.0 / (double) totalnodes;
x1 = -1.0 + mynode * h;
x2 = x1 + h;
y1 = -1.0;
y2 = 1.0;
my_SqPoints  = 0;
my_CiPoints  = 0;

for (i = 1; i <= n; i += totalnodes){
 x = rand(); x = x / RAND_MAX; x = x1 + x * (x2 - x1);
 y = rand(); y = y / RAND_MAX; y = y1 + y * (y2 - y1);
 my_SqPoints++;
 if ( ( x*x + y*y ) <= 1.0 ) my_CiPoints++;
}

Then we perform the reduction by doing

SqPoints = 0;
CiPoints = 0;
MPI_Reduce(&my_SqPoints, &SqPoints, 1, MPI_INT, MPI_SUM, 0,
    MPI_COMM_WORLD);
MPI_Reduce(&my_CiPoints, &CiPoints, 1, MPI_INT, MPI_SUM, 0,
    MPI_COMM_WORLD);

and print the approximation

if (mynode == 0){
pi = 4.0 * (double)CiPoints / (double)SqPoints;
printf("Pi is approximately %.16f, Error is %e\n"
    ,pi, fabs(pi - PI25DT));
}

Python version

Again we can implemente the same procedure in Python.

%%file montecarlo.py
"""
Computing pi with parallel quadrature formula
"""
import numpy
from mpi4py import MPI
import sys
import random

comm = MPI.COMM_WORLD
mynode = comm.Get_rank()
totalnodes = comm.Get_size()

truepi = 3.141592653589793238462643
dest = 0
pi = numpy.zeros(1)

# Initialize value of n only if this is rank 0
# we are not checking the input, if the user does something that
# has no meaning we are going to fail badly!
if mynode == 0:
    if len(sys.argv) == 1:
        n = numpy.full(1, 20, dtype=int) # default value
    else:
        n = numpy.full(1,int(sys.argv[1]),dtype=int)
else:
    n = numpy.zeros(1, dtype=int)

# Broadcast n to all processes
comm.Bcast(n, root=0)

# Compute local quantities
h  = 2.0 / totalnodes
x1 = -1.0 + mynode * h
x2 = x1 + h
y1 = -1.0
y2 = 1.0
my_SqPoints  = numpy.zeros(1, dtype=int)
my_CiPoints  = numpy.zeros(1, dtype=int)

for i in numpy.arange(1,n+1,totalnodes):
    x = random.random()
    x = x1 + x*(x2-x1)
    y = random.random()
    y = y1 + y*(y2-y1)
    my_SqPoints = my_SqPoints + 1
    if ( x**2 + y**2 <= 1.0 ):
        my_CiPoints = my_CiPoints + 1
    
SqPoints = numpy.zeros(1, dtype=int)
CiPoints = numpy.zeros(1, dtype=int)

# Send back to the root process the data
comm.Reduce(my_SqPoints, SqPoints, MPI.SUM, dest)
comm.Reduce(my_CiPoints, CiPoints, MPI.SUM, dest)

# Only print the result in process 0
if mynode == 0:
    pi = 4.0*float(CiPoints)/float(SqPoints)
    print('The Integral Sum =', pi," The Error is ",numpy.abs(pi-truepi))

Overwriting montecarlo.py

That we can execute as usual by doing

!mpiexec -np 4 python montecarlo.py 1000

The Integral Sum = 3.164  The Error is  0.02240734641020703

---

1

For some historical information about this idea: http://shorturl.at/mAWY8

A First Scientific Computation