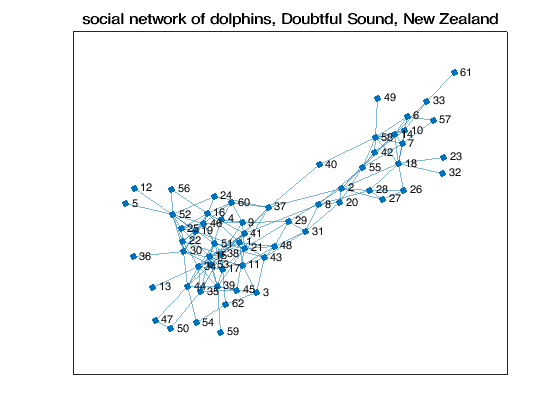
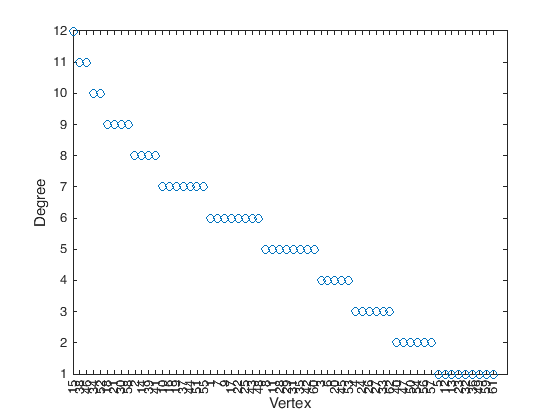
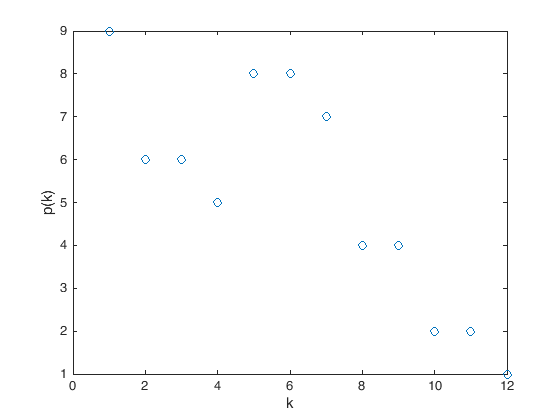
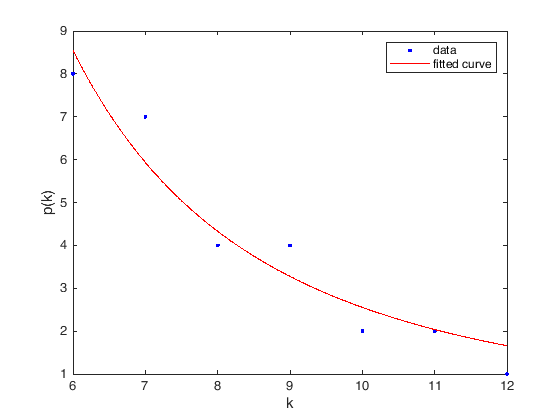
Graphs and Networks#

Understanding complex systems often requires a bottom-up analysis. This can be done by examining the elementary parts of the system individually and then by turning the analysis towards the connection between them. A natural way of performing this type of analysis is through the use of networks or graphs.

Definition 2

A graph \(G=(V,E)\) consists of a finite set \(V\) of vertices (or nodes) and a finite set \(E\) of edges, where each edge \(e\in E\) is of the form \(e=\{u,v\}\) with \(u,v\in V\).

And we will make here the following simplifying assumptions:

we do not allow any edge to be a self-loop, i.e., an edge that starts and ends at the same vertex,
we do not allow more than one edge between any pair of vertices,
unless mentioned otherwise we will mostly consider undirected edges, that is edge \(e = \{u,v\} = \{v,u\}\).

Now, let us fix some notation and nomenclature.

Definition 3

Two vertices, \(u\) and \(v\), are called adjacent if there is an edge, \(uv\), connecting them. We can express adjacency of \(u\) and \(v\) by writing \(u\sim v.\)

Definition 4

If \(v\) is a vertex in a graph \(G\), the degree of \(v\), denoted \(\operatorname{deg}(v)\), is the number of edges adjacent to \(v\).

Definition 5

A walk in a graph is a sequence of vertices and edges \(v_0\), \(e_1\), \(v_1\), \(e_2\), \(v_2\), \(\ldots\), \(v_{k-1}\), \(e_k\), \(v_k\) such that edge \(e_i\) connects vertices \(v_{i-1}\) and \(v_i\), for \(1 \leq i \leq k\).

Definition 6

A graph \(G\) is connected if for any two vertices \(u\) and \(v\) of \(G\), there is a walk in \(G\) from \(u\) to \(v\).

The first way to store a graph into a computer is as an adjacency matrix. Given a graph \(G\) with \(n\) vertices, we start by label them from \(1\) to \(n\), then the adjacency matrix representing this graph will be an \(n\times n\) matrix whose entries are either 0 or 1, specifically

\[\begin{split}A(i,j) = \begin{cases} 1, & (v_i,v_j) \in E,\\ 0, & \text{otherwise}. \end{cases}\end{split}\]

We now have much of the dictionary we need to start investigating some examples of graphs and networks that are used in applications. We will uncover some more information by working through the test cases.

Finding communities#

Let us start again from an example, we consider here some data from [vDKArguellesTico+14] related to the behavior of a specie of social birds that nest in communal chambers. These contains a set of networks constructed in the following way:

An individual was assigned to a given nest chamber once it had been observed to enter it, irrespective of the activity carried out, i.e. either building the nest chamber or roosting in it. A network ‘edge’ was drawn between individuals that used the same nest chambers either for roosting or nest-building at any given time within a series of observations at the same colony in the same year, either together in the nest chamber at the same time or at different times. These individuals werethus assumed to be associated.

We read from the data file the nodes, and edges of the network. The file (that we obtained from the Network Repository [RA15]) is not formatted as a CSV file, but has instead spaces to separate the data, thus we use the command dlmread, that generalizes the csvread command

data = dlmread('aves-wildbird-network-1.edges');

with this we have obtained a matrix with three columns and number of edges rows in which the first column represents the starting node, the second column the ending node, and the third one the edge weight. With this data we can build a graph

G = graph(data(:,1),data(:,2),data(:,3));

and then plot it

plot(G,'Layout',"force3");

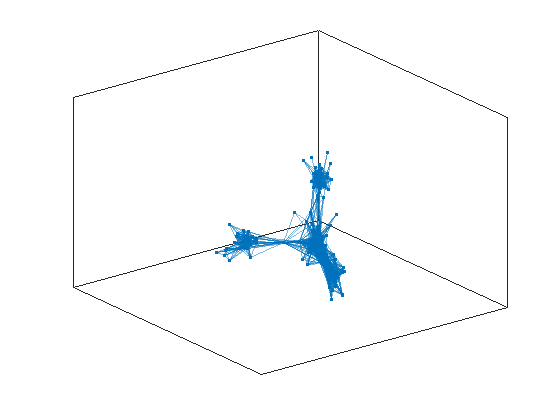
From the plot we suspect that we can identify two communities in our set of birds, but how can we do it mathematically? This task is called a task of community detection, and there are many algorithms and strategies for achieving it. We are going to focus here on a techinique that is called spectral clustering. First of all we need a particular representation of the network with a matrix called a Laplacian of the network:

L = laplacian(G);

Then we recover the spectral information by the command:

[v,l] = eigs(L,2,'smallestabs');

This gives us two vectors \(\mathbf{v}_1\) and \(\mathbf{v}_2\) and two values \(\lambda_1\) and \(\lambda_2\) such that

\[L \mathbf{v}_1 = \lambda_1 \mathbf{v}_1, \quad L \mathbf{v}_2 = \lambda_2 \mathbf{v}_2,\]

these are called, respectively, eigenvectors, and eigenvalues. If we inspect them we observe that \(v_1(i) > 0\) for all \(i = 1,\ldots,N\), and moreover it has a constant value. The second one, is the one we are actually interested in, this has both values that are \(> 0\) and \(< 0\). We are going to use them to determine the communities:

ind1 = find(v(:,2) > 0);
ind2 = find(v(:,2) < 0);

Now let us evidentiate the nodes on the graph

h = plot(G,'Layout',"force3");
highlight(h,ind1,"NodeColor",'red',"MarkerSize",6)
highlight(h,ind2,"NodeColor",'blue',"MarkerSize",6)

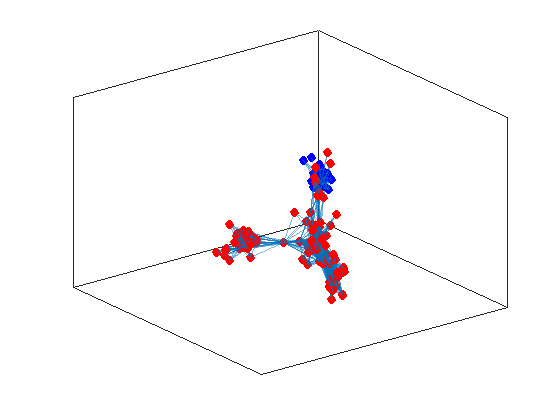
and as you can observe the procedure did evidentiate the two communities we were suspecting by working directly on the data. On the other hand, now that we look better at the data, we suspect that there could be more than two communities, the larger one seems to be splittable in two. We can try to identify larger number of communities, by computing more eigenvectors

[v,l] = eigs(L,3,'smallestabs');
idx = kmeans(v(:,2:3),3);
ind1 = find(idx == 1);
ind2 = find(idx == 2);
ind3 = find(idx == 3);
h = plot(G,'Layout',"force3");
highlight(h,ind1,"NodeColor",'red',"MarkerSize",6)
highlight(h,ind2,"NodeColor",'blue',"MarkerSize",6)
highlight(h,ind3,"NodeColor",'green',"MarkerSize",6)

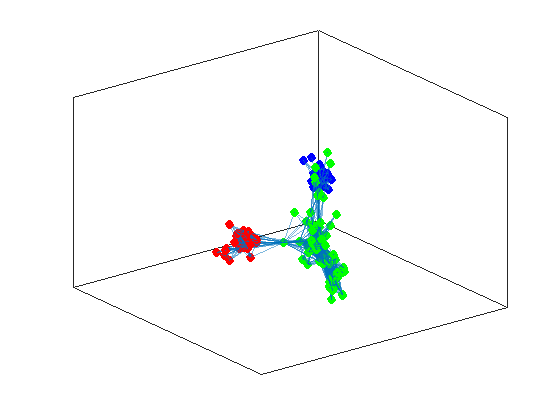
now we don’t have a clear cut between positive and negative values in a single vector, thus we have to employ another algorithm to do the separation for us. This is the \(K\)-means algorithm that returns as a vector of indexes for the corresponding communities.

Tip

\(K\)-means is a clustering method that uses the process of vector quantization, it was originally devised in the signal processing community with the aims of partitioning \(n\) observations into \(k\) clusters in which each observation belongs to the cluster with the nearest mean, i.e., the mean servs as a prototype of the cluster.

It can be formally expressed as the minimization problem

\[\arg\min_{\mathbf{S}=\{S_1,\ldots,S_k\}} \sum_{i=1}^{k}\sum_{\mathbf{x} \in S_i} \| \mathbf{x} - \mathbf{\mu}_i\|^2,\]

where we are given \(\{\mathbf{x}_1,\ldots,\mathbf{x}_n\}\) observations, to cluster in \(k\,(\leq n)\) groups \(\{S_1,\ldots,S_k\}\), and \(\mathbf{\mu}_i\) is the mean of the points in \(S_i\).

But how do we know if we haven’t lost some community in our analysis? To test this idea we can use another concept from graph theory that is called modularity.

Definition 7

Modularity is a measure of the structure of networks or graphs which measures the strength of division of a network into communities, it is computed as the fraction of the edges that fall within the given groups minus the expected fraction if edges were distributed at random.

There are several ways for computing this quantity, we give here a very straigthforward

function Q = modularity(A, g)
%% MODULARITY computes the modularity of the of the partition in group g of the
% graph with adjacency matrix A.

nCommunities = numel(unique(g));
nNodes = length(g);

e = zeros(nCommunities);
for i = 1:nNodes
    for j = 1:nNodes
        e(g(i), g(j)) = e(g(i), g(j)) + A(i, j);
    end
end
nEdges = sum(A(:));  % we could use nnz(A), but we want to take into account weights
a_out = sum(e, 2);   % out-degree
a_in = (sum(e, 1))'; % in-degree
a = a_in.*a_out/nEdges^2;
Q = trace(e)/nEdges - sum(a);

end

and we try to use it to evaluate the communities we have found

%% Analysis of Community Structure
addpath('matlabcodes')
data = dlmread('aves-wildbird-network-1.edges');
color = {'red','blue','magenta','green'};
G = graph(data(:,1),data(:,2),data(:,3));
L = laplacian(G);
for i = 1:3
    [v,l] = eigs(L,i+1,'smallestabs');
    groupvec = kmeans(v(:,2:i+1),i+1);
    figure(1)
    subplot(1,3,i);
    h = plot(G,'Layout',"force3");
    for j = 1:i+1
       ind = find(groupvec == j);
       highlight(h,ind,"NodeColor",color{j},"MarkerSize",6)
    end
    Q = modularity(adjacency(G),groupvec);
    title(['Modularity is ',string(Q)])
end
set(gcf,'Position',[-1984 426 1301 395]);

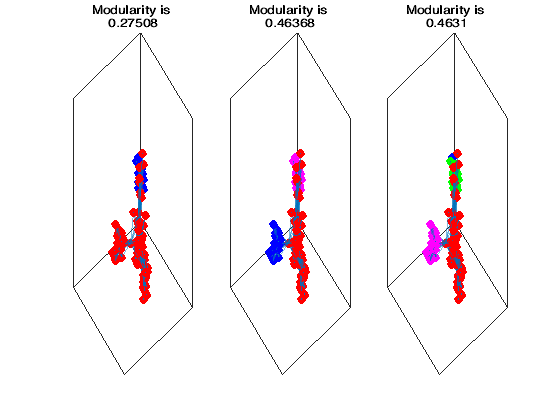
from which we observe that if we try to find more than three communities the modularity starts decreasing. Thus it seems that we are done with three communities for this dataset.

Exercise 8

We write a function that looks for in a graph up to \(n\) communities and returns the number of communities within \(n\) with the highest modularity.

function [groups,outmodularity,optimum] = findcommunities(G,k)
%%FINDCOMMUNITIES looks in G up to n communities and returns the number
%of communities within n with the highest modularity.
%   G = graph
%   k = maximum number of communities

if (k > G.numnodes)
    error("You cannot have more than number of nodes communities");
end
if (k < 2)
    error("You cannot have less than 2 communities");
end

% Allocate the space for the groups matrix of number of nodes rows and
% k-1 columns

% Allocate the space for the modularities: vector with k-1 entries

% Loop through the possible community size
% | Compute eigenvectors
% | Use k-means
% | Compute modularity
% end of the for loop

% Compute the index for which maximum modularity is obtained

end

You can test the algorithm on some of the networks on some Animal social networks.

Tip

To ensure that the function also automatically produces graphs highlighting the communities, the following two auxiliary codes can be used:

Generate maximally perceptually-distinct colors This function generates a set of colors which are distinguishable by reference to the “Lab” color space, which more closely matches human color perception than RGB.
neatly arrange subplots Sometimes a graphing function will not know in advance how many sub-plots are to be created. This function produces reasonable values for the row and column inputs to subplot given the number of desired sub-plots.

Centrality#

The next type of analysis we want to address is the computation of a node centrality score, this type of analysis can (usually) be done by employing some topological measures, i.e., that depends only on the connections of the nodes, to score nodes by their “importance”.

Definition 8

A graph Centrality measures are scalar values given to each node in the graph \(G = (V,E)\) to quantify its importance. The definition of what is important depends on the underlying model assumption.

Let us see some measures on a sample graph \(G = (V,E)\) that could be, e.g., the contact network ia-infect-hyper.mtx where nodes represent humans and edges between them represent proximity, i.e., a contact for a given period of time in the physical world; see [RA15].

addpath('./data')
data = dlmread('ia-infect-hyper.mtx',' ',2,0);
G = graph(data(:,1),data(:,2));
fprintf("G is a Network with %d nodes and %d edges.\n",G.numnodes,G.numedges);

G is a Network with 113 nodes and 2196 edges.

Degree centrality. It is defined as the number of node neighbors for each node in the graph. If the network is directed, we have two versions of this measure: the in-degree is the number of incoming edges, and the out-degree that is in turn the number of out-going edges. This is a local measure, that means that as a measure it doesn’t take neighbors connectivity into account. It can be interpreted as a form of popularity.

degree_centrality = G.degree;

Closeness centrality. This centrality measures node efficiency in terms of connection to other nodes. Is defined as the average length of the shortest path between the node and all other nodes in the graph, i.e., the more central a node is, the closer it is to all other nodes.

\[v \in V, \quad C(v) = \frac{1}{\sum_{w \in V} d(v,w)}.\]

closeness_centrality = centrality(G,"closeness");

Betweenness centrality. This measure quantifies the number of times a node acts as a bridge along the shortest path between two other nodes, that is, let us say that we want to compute it for a vertex \(v \in V\). We first compute all the shortest paths between each pair of vertices \((s,t)\), then for each of the couples we determine the fraction of shortest paths that pass through \(v\). The measure is then the sum this fraction over all pairs of vertices, succinctly

\[\begin{split}v \in V, \quad B(v) = \sum_{s \neq v \neq t \in V} \frac{\sigma_{st}(v)}{\sigma_{st}}, \; \begin{array}{l} \sigma_{st} = |\{ \text{shortest paths between s and t }\}|, \\ \sigma_{st}(v) = |\{ \text{shortest paths between s and t passing per v}\}|. \end{array}\end{split}\]

betweenness_centrality = centrality(G,"betweenness");

Eigenvector centrality. It assigns relative scores to all nodes in the network based on the assumption that “connections to important nodes matters more to the score of the node we are looking at than equal connections to low importance nodes”. This idea can be formalized in different ways. The first we consider is the case in which we use the eigenvector corresponding to the largest eigenvalue of the graph adjacency matrix.

eigenvector_centrality = centrality(G,"eigenvector");

PageRank. This is the algorithm used by Google Search to rank the web pages in their search engine results. The score given by this algorithm is a probability distribution representing the likelihood of randomly exploring the network and arriving at any particular page.

\[\mathbf{p} = \mathbf{p}\left(\gamma P + (1-\gamma) \mathbf{v}\mathbf{1}^T\right), \quad P = \operatorname{diag}(A\mathbf{1})^{-1}A,\; \gamma \in [0,1], \; \mathbf{1}^T\mathbf{v} = 1.\]

pagerank_centrality = centrality(G,"pagerank");

We can now try to look at the most-important nodes for the different measures. Since we are only interested in the ranking (and not in the actual value of the measure) we will make use of the sort function from MATLAB to get the information we want

[~,degree_rank] = sort(degree_centrality,"descend");
[~,closeness_rank] = sort(closeness_centrality,"descend");
[~,betweenness_rank] = sort(betweenness_centrality,"descend");
[~,eigenvector_rank] = sort(eigenvector_centrality,"descend");
[~,pagerank_rank] = sort(pagerank_centrality,"descend");

rankings = table(degree_rank,closeness_rank,betweenness_rank,...
    eigenvector_rank,pagerank_rank,'VariableNames',...
    {'Degree','Closeness','Betweenness','Eigenvector','PageRank'});
disp(head(rankings))

    Degree    Closeness    Betweenness    Eigenvector    PageRank

    ______    _________    ___________    ___________    ________

      30          30            30             30           30

      38          38            42            102           42

      42          42            33             38           38

     102         102            38             42          102

      33          33           102             33           33

      48          48            12             48           48

      12          12            48             34           12

      34          34            34             12           34

To compare the different rankings we can also look at the scatter plot of the rankings, e.g.,

figure(1)
subplot(1,2,1);
plot(degree_rank,closeness_rank,'o');
xlabel('Degree centrality')
ylabel('Closeness centrality')
axis square
subplot(1,2,2);
plot(degree_rank,eigenvector_rank,'o');
xlabel('Degree centrality')
ylabel('Eigenvector centrality')
axis square

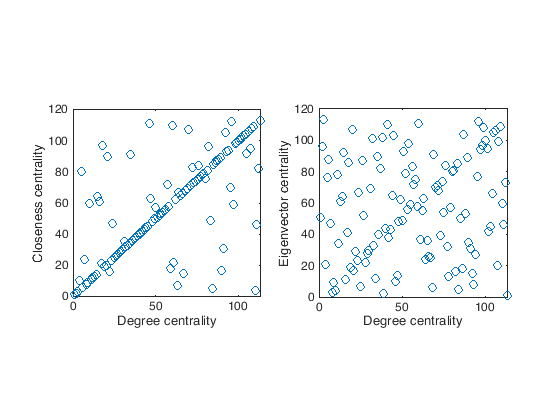
In general it would be better to have also a quantitative way of comparing the rankings. We can go for a statistical test, in this case a good solution is the Kendall \(\tau\) test.

The Kendall \(\tau\) coefficient is defined as:

\[\tau = \frac{(\text{number of concordant pairs}) - (\text{number of discordant pairs})}{ {n \choose 2} }.\]

Where \({n \choose 2} = {n (n-1) \over 2}\) is the binomial coefficient for the number of ways to choose two items from \(n\) items. We can compute it in MATLAB (together with the relevant \(p\)-value) by doing:

[tau,pval] = corr(degree_rank,closeness_rank,'type','Kendall');
fprintf("Degree vs Closeness tau = %f p-value = %e.\n",tau,pval);
[tau,pval] = corr(degree_rank,eigenvector_rank,'type','Kendall');
fprintf("Degree vs Eigenvector tau = %f p-value = %e.\n",tau,pval);

Degree vs Closeness tau = 0.581226 p-value = 7.253673e-20.

Degree vs Eigenvector tau = 0.099558 p-value = 1.185833e-01.

Warning

Every centrality measure is based on an assumption about the concept of importance, e.g, closeness and betweenness centralities define the importance as an evaluation of the information exchange efficiency within the networks. Others like the degree are purely local popularity measure, while the ones based on the eigenvectors tend to reward highly connected nodes. You should always select your measure while taking into account the model behind the choice.

Bibliography#

Lus03(1,2): David Lusseau. The emergent properties of a dolphin social network. Proceedings of the Royal Society of London. Series B: Biological Sciences, 270(suppl_2):S186–S188, 2003.
RA15(1,2): Ryan A. Rossi and Nesreen K. Ahmed. The network data repository with interactive graph analytics and visualization. In AAAI. 2015. URL: https://networkrepository.com.
vDKArguellesTico+14: Rene E van Dijk, Jennifer C Kaden, Araceli Argüelles-Ticó, Deborah A Dawson, Terry Burke, and Ben J Hatchwell. Cooperative investment in public goods is kin directed in communal nests of social birds. Ecology letters, 17(9):1141–1148, 2014.

Numerical recipes for environmental sciences with MATLAB

Graphs and Networks

Contents

Graphs and Networks#

Finding communities#

Centrality#

Bibliography#

Numerical recipes for environmental sciences with MATLAB

Graphs and Networks

Contents

Graphs and Networks#

A social network made of dolphins#

Finding communities#

Centrality#

Bibliography#