Laboratorio 10a : Il Metodo di Bisezione#

In questo laboratorio ci occuperemo del problema dell’individuazione degli zeri di una funzione continua \(f : \mathbb{R} \to \mathbb{R}\). Per farlo adopereremo il metodo di bisezione.

Per applicare il metodo abbiamo bisogno di un intervallo \([a,b] \subset \mathbb{R}\) per cui abbiamo che \(f(a)f(b) < 0\), ovvero per cui \(f(a)\) e \(f(b)\) assumono segni opposti.

Esercizio 1

Si implementi in una funzione MATLAB l’algoritmo di bisezione:

  1. Calcolare \(c\), punto medio dell’intervallo \([a,b]\), \(c = (a+b)/2\),

  2. Calcolare il valore della funzione al punto medio \(f(c)\),

  3. Se il criterio di convergenza è soddisfatto, restituire \(c\) e terminare le iterazioni

  4. Esaminare il segno di \(f(c)\) e rimpiazzare \((a,f(a))\) o \((b,f(b))\) con \((c,f(c))\) in modo che ci sia uno zero all’interno del nuovo intervallo.

Un template della funzione da implementare è il seguente:

function [c,residuo] = bisezione(f,a,b,maxit,tol)
%%BISEZIONE applica il metodo di bisezione per il calcolo di f(x) = 0
% Input:  f function handle della funzione di cui si cerca lo zero
%         a estremo sinistro dell'intervallo
%         b estremo destro dell'intervallo
%         maxit numero massimo di iterazioni
%         tol tolleranza richiesta su abs(f(c))
% Output: c vettore dei valori trovato dall'algoritmo
%         residuo vettore che contiene tutti i residui abs(f(c))


end

È importante che la funzione implementata

  • faccia il controllo degli input,

  • pre-allochi la memoria per i vettori c e residuo,

  • riduca al minimo le chiamate ad \(f(\cdot)\).

Per testare l’algoritmo possiamo usare il problema di test:

%% Test del metodo di bisezione

clear; clc; close all;

f = @(x) x.^3 -x -2;
a = 1;
b = 2;
maxit = 200;
tol = 1e-6;

[c,residuo] = bisezione(f,a,b,maxit,tol);

Convergenza#

L’analisi di convergenza per questo metodo vista a lezione ci dice che, se chiamiamo \(c_n\) l’iterata \(n\)-ma prodotta dal metodo e \(c\) la radice dell’equazione \(f(x) = 0\), allora

\[| c_n - c | \leq \frac{|b-a|}{2^n}.\]

Possiamo usare MATLAB per verificare che quanto abbiamo implementato sia consistente con quanto abbiamo dimostrato, per farlo elaboriamo ulteriormente l’esempio dell’Esercizio 1 con il seguente codice:

ctrue = 1.52137970680456757;
n = 1:length(residuo);
semilogy(n,residuo,'x--',...
    n,abs(c-ctrue),'ro--',...
    n,abs(b-a)./(2.^n),'k-','LineWidth',2)
xlabel('Iterazione n');
legend('Residuo del metodo','Errore Assoluto c','Bound');
axis tight

Che ci permette di produrre la figura Fig. 10, da cui osserviamo che l’errore assoluto sulla radice \(c\) segue l’andamento predetto dall’analisi teorica.

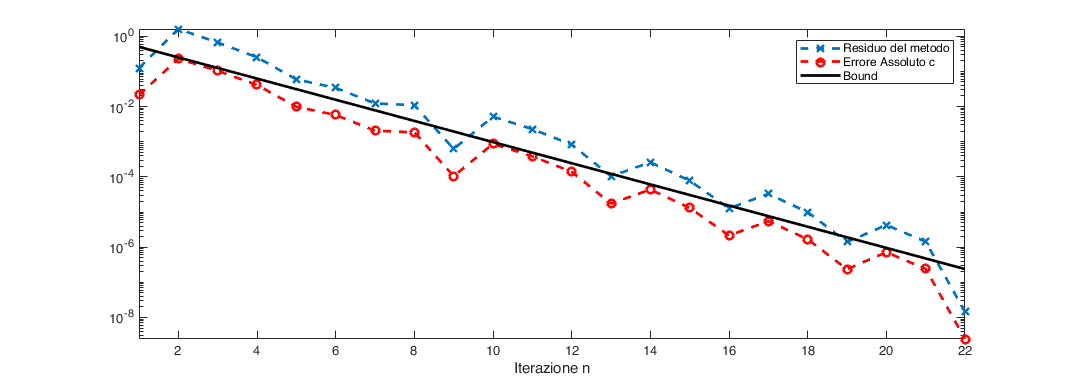
_images/bisezione-errore.png

Fig. 10 Errore nel metodo di bisezione per la soluzione del problema dell’Esercizio 1.#

Alcune note sul codice usato.

  • Per confrontare la convergenza sulla \(c_n\) abbiamo avuto necessità di avere un valore di \(c\) che abbiamo calcolato per altre via con 16 cifre di accuratezza,

  • Abbiamo usato la funzione semilogy per avere un grafico delle quantità in oggetto in cui abbiamo usato una scala logaritmica sull’asse delle \(y\) (in cui stavamo riportando gli errori).

Applicazioni#

Consideriamo alcune applicazioni ingegneristiche del problema di trovare lo zero di una funzione [Kiu15].

Esercizio 2

Un cavo d’acciao di lunghezza \(L\) è sospeso come mostrato nella figura:

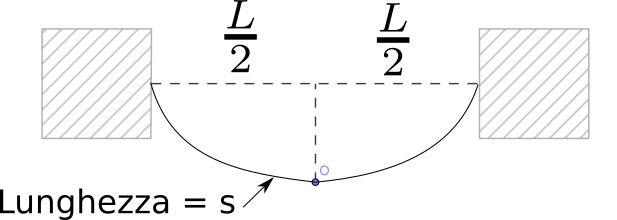
_images/cavo.png

Fig. 11 :name: cavo#

Sospensione di un cavo d’acciaio.

La massima trazione (stress tensile) nel cavo, che si verifica in corrispondenza dei supporti, è data dall’espressione

\[\sigma_{\text{max}} = \sigma_0 \cosh \beta, \qquad \beta = \frac{\gamma L}{2\sigma_0},\]

dove

  • \(\sigma_0 = \) è la tensione del cavo nel punto di origine \(O\),

  • \(\gamma\) peso del cavo per unità di volume,

  • \(L\) distanza tra i punti di supporto del cavo. Il rapporto lunghezza/spazio coperto dal cavo è correlato con \(\beta\) dall’espressione

\[\frac{s}{L} = \frac{1}{\beta} \sinh \beta.\]

Si calcoli \(\sigma_{\text{max}}\) se \(\gamma = 77 \times 10^3\,N/m^3\) (acciaio), \(L = 1000\,m\) e \(s = 1100\,m\).

Esercizio 3

Le frequenze naturali di una trave a sbalzo (cantilever) uniforme sono legate alle radici \(\beta_i\) dell’equazione

\[f(\beta) = \cosh \beta \cos \beta + 1 = 0,\]

dove

  • \(\beta_i^4 = (2\pi f_i)^2 \frac{mL^3}{E I}\),

  • \(f_i = i\)ma frequenza naturale della trave (misurata in Hz),

  • \(m = \) massa della trave,

  • \(L = \) lunghezza della trave,

  • \(E = \) modulo di elasticità,

  • \(I = \) momento di inerzia della sezione della trave.

Si determinano le due frequenze più basse di una trave d’acciaio lunga \(0.9 m\), con una sezione rettangolare larga \(25 mm\) e alta \(2.5 mm\). La densità della trave è di \(7850 kg/m^3\) e \(E = 200 GPa\).

Esercizio 4

L’equazione di Bernoulli per il flusso di un fluido attraverso un canale aperto con una piccola protuberanza (Fig. 13) è

\[\frac{Q^2}{2 g b^2 h_0^2} + h_0 = \frac{Q^2}{2 g b^2 h^2} + h + H,\]

dove

  • \(Q = 1.2 m^3/s\) portata del flusso,

  • \(g = 9.81 m/s^2\) accelerazione gravitazionale,

  • \(b = 1.9m\) larghezza del canale,

  • \(h_0 = 0.6m\) livello dell’acqua a monte,

  • \(H = 0.075 m\) altezza della protuberanza,

  • \(h\) = livello dell’acqua al di sopra della protuberanza.

Si determini il valore di \(h\).

Due funzioni di MATLAB#

Oltre le versioni che abbiamo implementato da noi, MATLAB dispone di alcune funzioni già implementate per risolvere il problema di trovare lo zero di una funzione.

La funzione generica per trovare lo zero di una funzione non lineare è la funzione

[x,fval,exitflag,output] = fzero(fun,x0,options)

dove

  • fun può essere un function handle, oppure una function salvata su di un file.

  • x0 è il punto di innesco per il metodo, se si ha una localizzazione della radice cercata è possibile passargli un vettore di due elementi x0 = [a,b] tali che \(f(a)f(b) < 0\).

  • options è una struttura che può essere omessa e che permette di comunicare all’algoritmo alcune opzioni ausiliare.

  • x contiene l’approssimazione dell”\(x\,:\,f(x) = 0\),

  • fval contiene il valore di \(f\) nell’approssimazione dello zero.

  • exitflag e output contengono invece delle informazioni sulla convergenza del metodo.

Alcuni esempi di opzioni sono:

options = optimset('PlotFcns',{@optimplotx,@optimplotfval}); % Stampa delle figure
                                                             % informative sulla
                                                             % procedura iterativa

oppure

options = optimset('Display','iter'); % mostra rapporto dettagliato delle iterazioni

Per vedere questa funzione all’opera potete provare il seguente esempio

fun = @(x) exp(-exp(-x)) - x; % Funzione di cui vogliamo trovare lo zero
x0 = [0 1]; % Intervallo in cui cercare la radice
options = optimset('Display','iter',...
                   'PlotFcns',{@optimplotx,@optimplotfval}); % Produci informazioni
[x fval exitflag output] = fzero(fun,x0,options)

Che ci restituirà le seguenti informazioni, dapprima una stampa iterazione per iterazione di quello che l’algoritmo sta facendo:

Func-count    x          f(x)             Procedure
	 2               1     -0.307799        initial
	 3        0.544459     0.0153522        interpolation
	 4        0.566101    0.00070708        interpolation
	 5        0.567143  -1.40255e-08        interpolation
	 6        0.567143   1.50013e-12        interpolation
	 7        0.567143             0        interpolation

Zero found in the interval [0, 1]

Successivamente, poiché non abbiamo chiuso con un ; l’istruzione leggiamo il valore dello zero, il valore della funzione in quel punto, la flag di uscita:

x =

	 0.5671


fval =

		0


exitflag =

		1

flag che ci viene tradotta nel campo message della struttura output, insieme ad un riassunto di quello che l’algoritmo ha fatto.

output =

 struct with fields:

	 intervaliterations: 0
					 iterations: 5
						funcCount: 7
						algorithm: 'bisection, interpolation'
							message: 'Zero found in the interval [0, 1]'

Vediamo invece la rappresentazione grafica di quanto ci è stato riassunto con 'display','iter' nella figura a lato.

Questa funzione applica una versione modificata di un algoritmo che non fa uso delle derivate da [Bre73].

Suggerimento

Si può provare a risolvere gli esercizi precedenti utilizzando invece che il metodo di bisezione implementato da noi la funzione fzero e confrontare i risultati in termini di tempi di calcolo e numero di valutazioni di funzione.

Per misurare il tempo intercorso in un blocco di istruzioni MATLAB si usano i comandi tic e toc:

tic;
% Blocco di istruzioni MATLAB
tempo = toc;
fprintf("Il tempo trascorso è: %1.2e (s).\n",tempo);

Zeri di polinomi#

Una famiglia di funzioni per cui è tipico dover calcolare tutti gli zeri sono i polinomi di grado \(n\) \(\mathbb{P}_n[x]\). A questo scopo esistono diversi algoritmi ad-hoc in genere basati su una riformulazione del problema come un opportuno problema di calcolo degli autovalori di una matrice. MATLAB ne implementa uno per mezzo del comando roots

r = roots(p)

dove

  • p è un vettore che contiene gli \(n+1\) coefficienti del polinomio \(p(x)\) a partire dal coefficiente di \(x^{n+1}\), cioè per \(p(x) = a_n x^{n} + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0,\) il vettore \(p\) è \(p = [a_n,a_{n-1},\ldots,a_1,a_0]\).

Pericolo

Il calcolo delle radici di un polinomio può essere un problema estremamente malcondizionato. Si consideri ad esempio il seguente polinomio:

\[p(x) = \prod_{i=1}^{20}(x-i) = x^{20}-210 x^{19}+20615 x^{18}-1256850 x^{17}+53327946 x^{16}-1672280820 x^{15}+40171771630 x^{14}-756111184500 x^{13}+11310276995381 x^{12}-135585182899530 x^{11}+1307535010540395 x^{10}-10142299865511450 x^9+63030812099294896 x^8-311333643161390640 x^7+1206647803780373360 x^6-3599979517947607200 x^5+8037811822645051776 x^4-12870931245150988800 x^3+13803759753640704000 x^2-8752948036761600000 x+2432902008176640000\]

le cui radici sono chiaramente \(i=1,2,\ldots,20\). Se andiamo ad applicare il nostro algoritmo

p = [1, -210, 20615, -1256850, 53327946, -1672280820, 40171771630, ...
-756111184500, 11310276995381, -135585182899530, 1307535010540395, ...
-10142299865511450, 63030812099294896, -311333643161390640, ...
1206647803780373360, -3599979517947607200, 8037811822645051776, ...
-12870931245150988800, 13803759753640704000, -8752948036761600000, ...
2432902008176640000];
r = roots(p);

troviamo:

r =

   19.9998
   19.0019
   17.9909
   17.0254
   15.9463
   15.0755
   13.9148
   13.0743
   11.9533
   11.0250
    9.9904
    9.0029
    7.9994
    7.0001
    6.0000
    5.0000
    4.0000
    3.0000
    2.0000
    1.0000

che è abbastanza vicino a quello che ci aspettavamo, tuttavia se proviamo a perturbare il coefficiente di \(x^{19}\) facendolo diventare da \(-210\) a \(-210 - 10^{-6}\) e replichiamo il comando roots otteniamo:

21.7491 + 0.0000i
20.1114 + 2.8284i
20.1114 - 2.8284i
16.7872 + 3.8754i
16.7872 - 3.8754i
13.7260 + 3.3928i
13.7260 - 3.3928i
11.4286 + 2.3089i
11.4286 - 2.3089i
 9.7385 + 1.1421i
 9.7385 - 1.1421i
 8.5965 + 0.0000i
 8.0736 + 0.0000i
 6.9976 + 0.0000i
 6.0000 + 0.0000i
 5.0000 + 0.0000i
 4.0000 + 0.0000i
 3.0000 + 0.0000i
 2.0000 + 0.0000i
 1.0000 + 0.0000i

che è sensibilmente diverso. Se avete la curiosità di leggere di più su questo argomento, il lavoro originale al riguardo è [Wil59].

Bibliografia#

Bre73

Richard P. Brent. Algorithms for minimization without derivatives. Prentice-Hall Series in Automatic Computation. Prentice-Hall, Inc., Englewood Cliffs, N.J., 1973.

Kiu15

Jaan Kiusalaas. Numerical Methods in Engineering with MATLAB®. Cambridge University Press, 3 edition, 2015. doi:10.1017/CBO9781316341599.

Wil59

J. H. Wilkinson. The evaluation of the zeros of ill-conditioned polynomials. I, II. Numer. Math., 1:150–180, 1959. URL: https://doi.org/10.1007/BF01386381, doi:10.1007/BF01386381.