Laboratorio 6 : Metodi di Quadratura

Compito dell’integrazione numerica, o quadratura è quello di approssimare il valore dell’integrale

\[\int_{a}^{b} f(x)\,{\rm d}x,\]

con la somma finita

\[I = \sum_{i=0}^{n} \omega_i f(x_i),\]

dove i nodi \(\{x_i\}_{i=0}^n\) e i pesi \(\{ \omega_i \}_{i=0}^{n}\) dipendono dalla particolare forma scelta. Come avete visto a lezione, le regole di quadratura provengono dalla scelta di un particolare polinomio interpolante per la funzione \(f\). Delle diverse famiglie di formule quadrature che esistono ci focalizzeremo qui sull’implementazione delle formule di Newton-Cotes.

Ricordiamo brevemente il funzionamento generale di questa procedura. Consideriamo l’integrale definito

\[\int_{a}^{b} f(x)\,{\rm d}x,\]

e dividiamo l’intervallo \((a,b)\) in \(n\) intervalli di uguale lunghezza

\[h = \frac{b-a}{n}, \quad x_{i} = a + i h, \; i=0,\ldots,n,\]

sostituiamo poi alla funzione \(f\) il suo polinomio interpolante in forma di Lagrange sui valori \(\{ (x_i,f(x_i))\}_{i=0}^{n}\)

\[P_{n}(x) = \sum_{i=0}^{n} f(x_i)\ell_i(x),\]

da cui otteniamo che

\[I = \int_{a}^{b} P_{n}(x)\,{\rm d}x = \sum_{i=0}^{n}\left[ f(x_i) \int_{a}^{b} \ell_{i}(x) \right] = \sum_{i=0}^{n} \omega_i f(x_i),\]

dove i pesi non sono nient’altro che gli integrali

\[\omega_i = \int_{a}^{b} \ell_i(x)\,{\rm d}x, \quad i=0,\ldots,n.\]

Vediamo e implementiamo ora alcune celebri formule di quadratura di questa forma.

Regola composita dei trapezi

Supponiamo di scegliere \(n=1\), ovvero \(h = b-a\) e quindi \(x_0 = a\), \(x_1 = b\), e quindi

\[\begin{split}w_0 = & -\frac{1}{h}\int_{a}^{b} (x-b)\,{\rm d}x = \frac{1}{2h}(b-a)^2 = \frac{h}{2},\\ w_1 = & \frac{1}{h}\int_{a}^{b} (x-a)\,{\rm d}x = \frac{1}{2h}(b-a)^2 = \frac{h}{2},\end{split}\]

da cui

\[I = \sum_{i=0}^{1} \omega_i f(x_i) = \frac{h}{2}(f(a)+f(b)),\]

e che è esattamente l’area del trapezio di altezza \(b-a\) e basi \(f(a)\) e \(f(b)\). L’errore per questa approssimazione, se \(f\) è due volte differenziabile, è dato da

\[E = O\left( \frac{h^3}{12} f''(\xi) \right),\]

dove \(\xi\) è un punto in \([a,b]\) e che quindi possiamo maggiorare con il massimo di \(f''(x)\) in \([a,b]\).

Facciamo una rapida verifica con MATLAB

f = @(x) sin(x);
Ix = @(x) -cos(x);
a = 0;
b = 1;
h = b - a;
I = h*(f(a)+f(b))/2;
Itrue = Ix(b)-Ix(a);
fprintf('|I - Itrue| = %e\n',abs(I-Itrue));
fprintf("Dovrebbe essere dell'ordine di: %e\n", h^3/12);

Questo ovviamente non ci è sufficiente, poiché non appena andiamo ad aumentare l’intervallo \([a,b]\) ( e quindi \(h\) ) su cui vogliamo calcolare l’integrale le cose peggiorano nettamente

f = @(x) sin(x);
Ix = @(x) -cos(x);
a = 0;
b = pi;
h = b - a;
I = h*(f(a)+f(b))/2;
Itrue = Ix(b)-Ix(a);
fprintf('|I - Itrue| = %e\n',abs(I-Itrue));
fprintf("Dovrebbe essere dell'ordine di: %e\n", h^3/12);

non abbiamo nemmeno una cifra significativa corretta.

Per risolvere questo inconveniente, possiamo passare ad utilizzare una composita. Dividiamo di nuovo l’intervallo \([a,b]\) in \(n\) sotto-intervalli di ampiezza \(h = (b-a)/n\) e approssimiamo su ogni sotto-intervallo l’integrale con la formula dei trapezi locale

\[I = \frac{h}{2} \sum_{i=0}^{n-1} \big(f(x_i) + f(x_{i+1})\big),\]

per cui si può ricavare una nuova stima dell’errore:

\[E = O\left(\frac{(b-a)h^2}{12} f''(\xi) \right),\]

dove \(\xi\) è sempre un valore nell’intervallo \([a,b]\).

Esercizio

Implementiamo la formula dei trapezi per una funzione \(f\) utilizzando il seguente prototipo

function I = trapezi(f,a,b,n)
%% TRAPEZI questa funzione implementa il metodo dei trapezi per la
% funzione f sull'intervallo a,b con n intervalli.
%   INPUT: f function handle dell'integrando,
%          a,b estremi dell'intervallo di integrazione
%          n numero di intervalli

end

• Si cerchi di minimizzare il numero di chiamate alla funzione \(f\) della routine,

• Un comando utile per questo esercizio è il comando linspace,

• Si scriva un codice che non utilizza cicli for.

Per testare l’implementazione si può provare a valutare l’integrale:

\[\pi = 4 \int_{0}^{1} \sqrt{1-x^2}\,{\rm d}x,\]

con

%% Test del metodo dei Trapezi

clear; clc; close all;

f = @(x) 4*sqrt(1-x.^2);
a = 0;
b = 1;

n = 9;
I = trapezi(f,a,b,n);

fprintf('Errore: %e\n',abs(pi-I)/pi);

Cerchiamo ora di verificare il comportamento della formula rispetto alla stima dell’errore che abbiamo ottenuto dalla teoria. Valutiamo che succede per l’integrale dell’esempio:

\[\pi = 4 \int_{0}^{1} \sqrt{1-x^2}\,{\rm d}x,\]

Proviamo a stimare l’errore in maniera numerica e a confrontarlo con il comportamento che ci aspettiamo dalla teoria:

n = logspace(1,4,4)-1;
errore = [];

for nval = n
    I = trapezi(f,a,b,nval);
    errore = [errore,abs(I-pi)/pi];
end

h = (b-a)./n;
err = (b-a)*h.^2/12;

figure(1)
loglog(n,errore,'o-',n,err/errore(1),'r--','LineWidth',2);
xlabel('n');
ylabel('Errore');
legend({'Errore Misurato','Stima'},'FontSize',14)

Errore regola dei trapezi

Errore per l’integrale

\[\pi = 4 \int_{0}^{1} \sqrt{1-x^2}\,{\rm d}x,\]

Errore per l’integrale

\[\int_0^3 x^2 \sin ^3(x) \, {\rm d}x\]

La stima non sembra particolarmente soddisfacente, ma siamo sicuri di poterla applicare? Calcoliamo la derivata seconda della nostra funzione integranda:

\[f''(t) = 4 \left(-\frac{t^2}{\left(1-t^2\right)^{3/2}}-\frac{1}{\sqrt{1-t^2}}\right) = \frac{-4}{\left(1-t^2\right)^{3/2}}\]

per cui abbiamo che:

\[\underset{t\to 1^-}{\text{lim}}\frac{-4}{\left(1-t^2\right)^{3/2}} = -\infty\]

ovvero, non possiamo limitare \(f''(\xi)\) nell’intervallo di integrazione.

Proviamo con una funzione diversa, ad esempio:

\[\begin{split}I = \int_0^3 x^2 \sin ^3(x) \, {\rm d}x = & \frac{1}{108} \left.-81 \left(x^2-2\right) \cos (x)+\left(9 x^2-2\right) \cos (3 x)-6 x (\sin (3 x)-27 \sin (x))\right|_{0}^{3} \\ = & \frac{1}{108} (-160+486 \sin (3)-18 \sin (9)-567 \cos (3)+79 \cos (9)),\end{split}\]

per cui la derivata seconda ha la regolarità necessaria

\[\begin{split}f''(x) = & x^2 \left(6 \sin (x) \cos ^2(x)-3 \sin ^3(x)\right)+2 \sin ^3(x)+12 x \sin ^2(x) \cos (x) \\ = & \frac{1}{2} \sin (x) \left(3 x^2+\left(9 x^2-2\right) \cos (2 x)+12 x \sin (2 x)+2\right)\end{split}\]

e si osserva che \(|f''(x)| < 10\) per \(x \in [0,3]\). Vediamo che succede numericamente:

f = @(x) x.^2.*sin(x).^3;
a = 0;
b = 3;
Itrue = 3.615857833947287;

n = logspace(1,4,4)-1;
errore = [];

for nval = n
    I = trapezi(f,a,b,nval);
    errore = [errore,abs(I-Itrue)/Itrue];
end

h = (b-a)./n;
err = 10*(b-a)*h.^2/12;

figure(2)
loglog(n,errore,'o-',n,err,'r--','LineWidth',2);
xlabel('n');
ylabel('Errore');
legend({'Errore Misurato','Stima'},'FontSize',14)

Avvertimento

Questa stima dell’errore è solo una prima approssimazione, in realtà è possibile ottenere stime più precise coinvolgendo termini di ordine superiore. Per i nostri scopi è sufficiente, ma sappiate che si può indagare più in profondità la questione.

Una versione ricorsiva

Supponiamo di aver scelto un valore di \(n\) per il nostro integrale, ma che alla fine del calcolo il valore ottenuto non abbia l’accuratezza che desideravamo. Quello che possiamo fare è scegliere un nuovo valore di \(n\) e calcolare di nuovo l’integrale. Questo, tuttavia, ci richiede di fare di nuovo tutte le valutazioni di funzione perché ad un nuovo \(n\) corrispondono nodi nuovi.

Possiamo recuperare in qualche modo parte dello sforzo?

Chiamiamo \(I_k\) l’integrale valutato con la regola composita dei trapezi usando \(2^{k-1}\) intervalli. Ora, se passiamo da \(k\) a \(k+1\) il numero di intervalli è raddoppiato.

Chiamiamo \(H = b - a\) e scriviamo la regola dei trapezi per i primi \(k\)

\[\begin{split}k = 1, &\quad I_1 = \frac{H}{2}[f(a) + f(b)],\\ k = 2, &\quad I_2 = \frac{H}{4}\left[ f(a) + 2 f\left(a + \frac{H}{2} \right) + f(b) \right] \\ &\quad\; = \frac{1}{2} I_1 + f\left(a + \frac{H}{2}\right)\frac{H}{2}, \\ k = 3, &\quad I_3 = \frac{H}{8}\left[ f(a) + 2 f\left(a + \frac{H}{4}\right) + 2 f\left(a + \frac{H}{2}\right) + 2 f\left(a + \frac{3H}{4}\right) + f(b) \right] \\ &\quad\; = \frac{1}{2} I_2 + \frac{H}{4}\left[f\left(a + \frac{H}{4}\right) + f\left(a + \frac{3H}{4}\right)\right].\end{split}\]

Con un po” di intuizione, possiamo scrivere per \(k > 1\)

\[I_k = \frac{1}{2}I_{k-1} + \frac{H}{2^{k-1}} \sum_{i=1}^{2^{k-2}} f \left[ a + \frac{(2i-1)H}{2^{k-1}} \right], \quad k=2,3,\ldots\]

Suggerimento

Qual è il vantaggio di questa scelta? La somma contiene solo nodi creati ad ogni nuovo raddoppio!

Ovvero, il calcolo della sequenza \(I_1, I_2, I_3, \ldots, I_k\) costa esattamente lo stesso numero di operazioni sia che si faccia il calcolo tutto insieme, sia che si calcolino separatamente tutti gli \(I_k\) uno dopo l’altro.

Il vantaggio dell’uso di questa forma della regola dei trapezi ricorsiva è che ci consente di monitorare la convergenza e terminare il processo quando la differenza tra \(I_{k-1}\) e \(I_k\) diventa sufficientemente piccola.

Per implementare l’algoritmo in modo ricorsivo, riscriviamo la formula in termini del valore di \(h\) come:

(7)\[I(h) = \frac{1}{2}I(2h) + h \sum f(x_{\text{new}}), \quad h = \frac{H}{n-1}.\]

Esercizio

Separiamo la funzione ricorsiva in due parti, la prima è quella che calcola \(I(h)\), dato \(I(2h)\), usando l’equazione (7) e chiamiamola trapezir

function Ih = trapezir(f,a,b,I2h,k)
%%TRAPEZIR implementa l'algoritmo ricorsivo della regola dei
%trapezi.
%   INPUT:  f = handle della funzione da integrare,
%           a,b = limiti di integrazione
%           I2h = integrale su 2^{k-1} intervalli
%           k  = livello di ricorsione
%   OUTPUT: Ih = integrale su 2^k intervalli

end

Una volta che la parte computazionale è stata completata possiamo mettere insieme la funzione ricorsiva

function I = trapeziricorsiva(f,a,b,kmax,tol)
%% TRAPEZIRICORSIVA calcola l'integrale di f tra a e b in modo
% ricorsivo. L'integrazione si ferma quando la differenza tra due
% ricorsioni successive è minore della tolleranza richiesta.
%   INPUT:  f = handle della funzione di integrare,
%           a,b = estremi di integrazione
%           kmax = massimo numero di livello di ricorsione
%           tol = tolleranza tra due livelli di ricorsione successivi

I2h = 0; k = 1;

Ih = trapezir(f,a,b,I2h,k);
fprintf('k = 1 Ih = %1.16f\n',Ih);

for k = 2:kmax
   I2h = Ih;
   Ih = trapezir(f,a,b,I2h,k);
   fprintf('k = %d Ih = %1.16f\n',k,Ih);
   if abs(Ih - I2h) < tol
       I = Ih;
       return
   end
end
warning("Non abbiamo raggiunto la tolleranza richiesta!");
I = Ih;

end

Dopo averlo fatto la testiamo sullo stesso integrale del caso precedente

%% Test della funzione ricorsiva dei trapezi

clear; clc; close all;

f = @(x) x.^2.*sin(x).^3;
a = 0;
b = 3;
Itrue = 3.615857833947287;
tol = 1e-9;
kmax = 20;

I = trapeziricorsiva(f,a,b,kmax,tol);
fprintf("\n\tL'errore è %e\n",abs(I - Itrue)/Itrue);

Formula di Simpson

La formula di quadratura di Simpson può essere ottenuta di nuovo come una formula di Newton-Cotes con \(n = 2\). Laddove nel caso dei trapezi avevamo fissato una interpolate lineare, questa volta abbiamo scelto una interpolante quadratica attraverso tre nodi adiacenti.

Possiamo ricavarla direttamente dalla definizione su un solo intervallo \([a,b]\) con i nodi

\[x_0 = a, \quad x_1 = \frac{a+b}{2}, \quad x_2 = b,\]

da cui abbiamo che i pesi si ottengono come

\[\begin{split}\omega_0 = \int_{a}^{b} \ell_0(x)\,{\rm d}x = \frac{h}{6}, \\ \omega_1 = \int_{a}^{b} \ell_1(x)\,{\rm d}x = \frac{2h}{3}, \\ \omega_2 = \int_{a}^{b} \ell_2(x)\,{\rm d}x = \frac{h}{6},\end{split}\]

e quindi

\[I = \sum_{i=0}^{2} \omega_i f(x_i) = \frac{h}{6}\left[ f(a) + 4f\left(\frac{a+b}{2}\right)+f(b)\right].\]

Suggerimento

Per calcolare gli integrali \(\omega_i\) è conveniente fare un cambio di variabili ponendo l’origine dell’intervallo di integrazione su \(x_1\). In questo modo i nodi diventano \(\{-h,0,h\}\) e gli integrali sono più semplici da calcolare.

Pericolo

La regola di Simpson che abbiamo scritto richiede che il numero di intervalli sia pari, ovvero che il numero di nodi sia dispari. Se vogliamo ammettere un qualunque numero di intervalli \(n\), è necessario che il primo (o l’ultimo) intervallo usi 4 invece che 3 punti.

Per l’implementazione seguente ci limiteremo al caso di nodi dispari, ovvero di intervalli pari.

Con calcoli analoghi a quelli che avete visto per la formula dei trapezi si può ottenere una prima stima dell’errore anche per la formula di Simpson. Infatti si ha che l’errore si comporta come

\[E = O\left( (b-a)\frac{h^4}{180} f^{(iv)}(\xi) \right),\]

per \(\xi\) un punto nell’intervallo \([a,b]\).

Esercizio.

Si implementi la versione composita della regola di Simpson per il calcolo di un integrale secondo il seguente prototipo

function I = simpson(f,a,b,n)
%%SIMPSON calcolo dell'integrale della funzione f tra a e b mediante la
% formula di Simpson.
%   INPUT:  f = handle della funzione di integrare,
%           a,b = estremi di integrazione
%           n numero di intervalli

if mod(n+1,2) ~= 1
    error('n deve essere pari');
end

end

Che possiamo testare con:

%% Test della formula di quadratura di Simpson

f = @(x) x.^2.*sin(x).^3;
a = 0;
b = 3;
Itrue = 3.615857833947287;

n = logspace(1,4,4);
errore = [];

for nval = n
    I = simpson(f,a,b,nval);
    errore = [errore,abs(I-Itrue)/Itrue];
end

h = (b-a)./n;
err = 200*(b-a)*h.^4/180;

figure(2)
loglog(n,errore,'o-',n,err,'r--','LineWidth',2);
xlabel('n');
ylabel('Errore');
legend({'Errore Misurato','Stima'},'FontSize',14)

Dove nella stima dell’errore 24*(b-a)*h.^4/180, abbiamo sfruttato il fatto che

\[\frac{d ^4\left(x^2 \sin (x)^3\right)}{d x^4} = x^2 \left(21 \sin ^3(x)-60 \sin (x) \cos ^2(x)\right)+8 x \left(6 \cos ^3(x)-21 \sin ^2(x) \cos (x)\right)+12 \left(6 \sin (x) \cos ^2(x)-3 \sin ^3(x)\right),\]

che in \([0,3]\) è maggiorata da \(200\).

Errore di quadratura Simpson

Errore per la formula di Simpson.

Possiamo quindi confrontare gli errori di quadratura ottenuti per le due formule stampandoli sullo stesso grafico

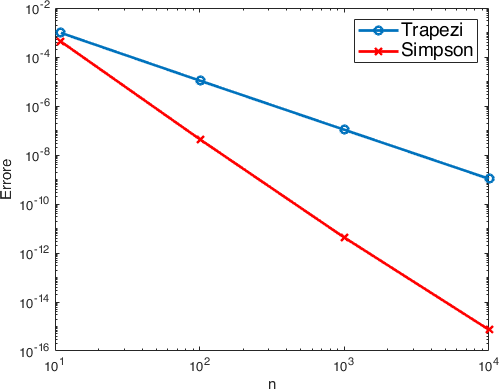
Fig. 4 Confronto tra l’errore relativo compiuto con la formula dei Trapezi e quello ottenuto con la formula di Simpson.

da cui osserviamo il comportamento che ci aspettavamo considerata l’analisi dell’errore.

Le funzioni di quadratura di MATLAB

MATLAB offre diverse funzioni per il calcolo di integrali. La prima da considerare è la funzione quad, dal cui help leggiamo

quad   Numerically evaluate integral, adaptive Simpson quadrature.
   Q = quad(FUN,A,B) tries to approximate the integral of scalar-valued
   function FUN from A to B to within an error of 1.e-6 using recursive
   adaptive Simpson quadrature. FUN is a function handle. The function
   Y=FUN(X) should accept a vector argument X and return a vector result
   Y, the integrand evaluated at each element of X.

   Q = quad(FUN,A,B,TOL) uses an absolute error tolerance of TOL
   instead of the default, which is 1.e-6.  Larger values of TOL
   result in fewer function evaluations and faster computation,
   but less accurate results.  The quad function in MATLAB 5.3 used
   a less reliable algorithm and a default tolerance of 1.e-3.

   Q = quad(FUN,A,B,TOL,TRACE) with non-zero TRACE shows the values
   of [fcnt a b-a Q] during the recursion. Use [] as a placeholder to
   obtain the default value of TOL.

Questa applica la quadratura di Simpson che abbiamo visto nella sezione precedente sfruttando la tecnica ricorsiva che abbiamo visto, applicato e implementato nel caso della regola dei trapezi.

Quest’ultima invece è implementata dal comando trapz, dal cui help leggiamo

trapz  Trapezoidal numerical integration.
   Z = trapz(Y) computes an approximation of the integral of Y via
   the trapezoidal method (with unit spacing).  To compute the integral
   for spacing different from one, multiply Z by the spacing increment.

   For vectors, trapz(Y) is the integral of Y. For matrices, trapz(Y)
   is a row vector with the integral over each column. For N-D
   arrays, trapz(Y) works across the first non-singleton dimension.

   Z = trapz(X,Y) computes the integral of Y with respect to X using the
   trapezoidal method. X can be a scalar or a vector with the same length
   as the first non-singleton dimension in Y. trapz operates along this
   dimension. If X is scalar, then trapz(X,Y) is equivalent to X*trapz(Y).

L’ultima funzione che vogliamo menzionare è integral che, in realtà, sostituisce la funzione quad che è in realtà deprecata. Questa applica una formula di quadratura adattiva e permette in realtà di calcolare anche integrali complessi, di funzioni con singolarità e regolare le tolleranze

integral  Numerically evaluate integral.
   Q = integral(FUN,A,B) approximates the integral of function FUN from A
   to B using global adaptive quadrature and default error tolerances.

   FUN must be a function handle. A and B can be -Inf or Inf. If both are
   finite, they can be complex. If at least one is complex, integral
   approximates the path integral from A to B over a straight line path.

   For scalar-valued problems the function Y = FUN(X) must accept a vector
   argument X and return a vector result Y, the integrand function
   evaluated at each element of X. For array-valued problems (see the
   'ArrayValued' option below) FUN must accept a scalar and return an
   array of values.

Di questa funzione sono disponibili anche le funzioni per il calcolo di integrali di funzioni in 2 e 3 variabili chiamate, rispettivamente, integral2 e integral3.

Applicazioni ed esercizi

Consideriamo alcuni esercizi sulla quadratura numerica da [Kiu15].

Accelerazione di una macchina

La Tabella 9 riporta la potenza \(P\) fornita alle ruote motrici di una macchina come funzione della velocità \(v\). Se la massa della macchina è \(m = 2000\,kg\), si determini l’intervallo \(\Delta t\) che serve alla macchina per accelerare da \(1\,m/s\) a \(6\,m/s\) utilizzando la regola dei trapezi implementata in trapz.

Tabella 9 Potenza e velocità

\(v\,(m/s)\)	\(P\,(kW)\)
0	0
1.0	4.7
1.8	12.2
2.4	19.0
3.5	31.8
4.4	40.1
5.1	43.8
6.0	43.2

Suggerimento

La funzione di cui calcolare l’integrale si può ottenere dalla seconda legge della dinamica e dalla definizione di potenza:

\[\Delta t = m \int_{1 s}^{6 s} (v/P)\,{\rm d}v.\]

Esercizio

Si calcoli l’integrale

\[I = \int_{1}^{+\infty} \frac{{\rm d}x}{1+x^4} = \frac{\pi -2 \coth ^{-1}\left(\sqrt{2}\right)}{4 \sqrt{2}},\]

con la regola dei trapezi e si paragoni il risultato con il valore esatto.

Si applichi un cambio di variabili…

Per riportare l’integrale su di un intervallo finito si applichi il cambio di variabili \(x^3 = 1/t\).

Esercizio

Il periodo di un pendolo semplice di lunghezza \(L\) è \(\tau = 4 \sqrt{L/g} h(\theta_0)\), dove \(g\) è l’accelerazione di gravità, \(\theta_0\) rappresenta l’ampiezza angolare e

\[h(\theta_0) = \int_{0}^{\pi/2} \frac{ {\rm d}\theta }{\sqrt{1- \sin^2(\theta_0/2)\sin^2(\theta)}}.\]

Si calcolino i periodi per \(h(15 \text{ deg})\), \(h(30 \text{ deg})\), \(h(45 \text{ deg})\) con la formula di Simpson e si paragonino all’approssimazione per piccoli angoli con \(h = \frac{\pi}{2}\). Cosa si osserva?

Bibliografia

Kiu15

Jaan Kiusalaas. Numerical Methods in Engineering with MATLAB®. Cambridge University Press, 3 edition, 2015. doi:10.1017/CBO9781316341599.