Laboratorio 2 : Introduzione a MATLAB - II

Array e Matrici

Abbiamo discusso fino ad ora l’utilizzo di variabili scalari, tuttavia in MATLAB i dati sono rappresentati in maniera naturale come matrici, array e, più in generale, tensori. È possibile applicare tutte le operazioni dell’algebra lineare agli array, in più si possono creare griglie comuni, combinare array esistenti, manipolare la forma e il contenuto di un array e utilizzare diverse modalità di indicizzazione per accedere ai loro elementi.

In realtà, abbiamo già surrettiziamente lavorato con degli array, poiché in MATLAB anche le variabili scalari non sono nient’altro che array unidimensionali, in notazione matematica un \(a \in \mathbb{R}\) è sempre un \(a \in \mathbb{R}^{1\times 1}\). Infatti se scriviamo nella command window:

a = 100;
whos a

il sistema ci restituirà

Name      Size            Bytes  Class     Attributes

a         1x1                 8  double   

Immaginiamo ora di disporre di uno specifico insieme di dati, che vogliamo disporre in una matrice. Possiamo farlo utilizzando la semantica delle parentesi quadre [ ].

Una singola riga di dati contiene spazi o virgole , tra gli elementi e fa uso di un punto e virgola ; per separare le righe.

Ad esempio, se vogliamo crea una singola riga di tre elementi numerici

v = [ 1 2 3]

oppure

v = [ 1, 2, 3]

La dimensione della matrice risultante è 1 per 3, poiché ha una riga e tre colonne. Una matrice di questa forma viene definita vettore riga e se chiamiamo la funzione isrow(v) ci vediamo rispondere

ans =

  logical

   1

Similmente, possiamo costuire un vettore colonna come

w = [ 1; 2; 3]

per cui abbiamo che invece iscolumn(w) ci restituirà

ans =

  logical

   1

Più in generale, possiamo costruire una matrice di \(4 \times 4\) elementi come

A = [ 1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]

oppure come

A = [ 1, 2, 3, 4; 5, 6, 7, 8; 9, 10, 11, 12; 13, 14, 15, 16]

o

A = [ 1, 2, 3, 4
      5, 6, 7, 8
      9, 10, 11, 12
      13, 14, 15, 16]

In tutti i casi ci vedremo restituire

A =

     1     2     3     4
     5     6     7     8
     9    10    11    12
    13    14    15    16

Possiamo indagare le dimensioni di una matrice mediante la funzione size(A), che nel caso precedente ci restituirà

ans =

     4     4

Costruttori predefiniti

Costruire matrici semplicemente inserendo i valori all’interno in sequenza o in maniera esplicita è chiaramente scomodo (e molto noioso). A questo scopo MATLAB possiede i costruttori riportati in Tabella 2.

Tabella 2 Costruttori per array e matrici.

Funzione	Operazione
zeros	Crea un array di tutti zeri Per costruire la matrice \(0 = (O)_{i,j}\) \(i,j=1,\ldots,n\) scriviamo O = zeros(n,m);
ones	Crea un array di tutti uno Per costruire la matrice \(1 = (E)_{i,j}\) \(i,j=1,\ldots,n\) scriviamo E = ones(n,m);
rand	Crea un array di numeri casuali uniformemente distribuiti in \([0,1]\). R = rand(n,m); Possiamo generare numeri uniformemente distribuiti nell’intervallo \([a,b]\) come R = a + (b-a).*rand(n,m);
eye	Matrice identità costruisce la matrice identità \((I)_{i,i} = 1\), \(i=1,\ldots,n\) e \(0\) altrimenti I = eye(n).
diag	Crea una matrice diagonale o estrae gli elementi diagonali di una matrice data. Se v è un vettore di lunghezza \(n\), allora diag(v) è una matrice la cui diagonale principale è data dagli elementi di v. Se A è una matrice allora diag(v) è un vettore che contiene gli elementi della diagonale principale di \(A\).

Altre funzioni dello stesso tipo sono true, false, blkdiag e i loro funzionamento può essere esplorato mediante la funzione help.

Il secondo insieme di funzioni estremamente utile per costruire matrici è quello che si occupa di gestire le concatenazioni. Queste possono essere ottenute sia utilizzando la notazione con le parentesi quadre [ ], ad esempio,

A = rand(5,5);
B = rand(5,10);
C = [A,B];

costruisce a partire dalle matrici \(A \in \mathbb{R}^{5 \times 5}\), \(B \in \mathbb{R}^{5\times 10}\), la matrice \(C \in \mathbb{R}^{5\times 15}\) ottenuta ponendo una accanto alle altre tutte le colonne di \(A\) seguite da quelle di \(B\). Alla stesso modo, si può ottenere la concatenazione verticale come

A = rand(8,8);
B = rand(12,8);
C = [A;B];

che genererà la matrice \(C \in \mathbb{R}^{20,8}\) ottenuta impilando tutte le righe di \(A\) seguite dalle righe di \(B\).

Pericolo

Le operazioni di concatenazione devono essere fatte tra matrici di dimensione compatibile, non possono esserci «avanzi» tra le dimensioni in oggetto. Per provare ad ottenere un errore si esegua:

A = rand(5,5);
B = rand(5,10);
C = [A;B];

che restituirà

Error using vertcat
Dimensions of arrays being concatenated are not consistent.

Al posto della notazione con le parentesi quadre è possibile fare uso delle funzioni horzcat e vertcat che corrispondono, rispettivamente, alle concatenazioni della forma [,] e [;].

Se vogliamo costruire invece una matrice diagonale a blocchi a partire dai blocchi diagonali possiamo utilizzare la funzione blkdiag il cui help ci restituisce esattamente

blkdiag  Block diagonal concatenation of matrix input arguments.

                                   |A 0 .. 0|
   Y = blkdiag(A,B,...)  produces  |0 B .. 0|
                                   |0 0 ..  |

   Class support for inputs:
      float: double, single
      integer: uint8, int8, uint16, int16, uint32, int32, uint64, int64
      char, logical

Slicing: accedere agli elementi

Il modo più comune di accedere ad un determinato elemento di un array o di una matrice è quello di specificare esplicitamente gli indici degli elementi. Ad esempio, per accedere a un singolo elemento di una matrice, specificare il numero di riga seguito dal numero di colonna dell’elemento:

A = [ 1 2 3 4
      17 8 2 1];
A(2,1)

che stamperà nella command window 17, cioè l’elemento in posizione riga 2 e colonna 1 di A (\(a_{2,1}\)).

Possiamo anche fare riferimento a più elementi alla volta specificando i loro indici in un vettore. Ad esempio, accediamo al primo e al quarto elemento della seconda riga della A precedente, facendo

A(2,[1,4])

che restituirà

ans =

    17     1

Per accedere agli elementi in un intervallo di righe o colonne, è possibile utilizzare l’operatore due punti :. Ad esempio, possiamo accedere accedi agli elementi dalla prima alla quinta riga e dalla seconda alla sesta colonna di una matrice \(A\) come

A = rand(10,10);
A(1:5,2:6)

Nel caso si voglia scorrere fino al termine di una dimensione è possibile sostituire il valore di destra nei : con la parola chiave end, ad esempio:

A(1:5,2:end)

Invece l’utilizzo di : senza valori di inizio/fine estrae tutte le entrate della dimensione relativa, ad esempio, 5 colonna, A(:,5), oppure colonne dalla quarta alla settima, A(:,4:7).

Nota

In generale, si può utilizzare l’indicizzazione per accedere agli elementi di qualsiasi array in MATLAB indipendentemente dal tipo di dati o dalle dimensioni.

L’ultimo modo di fare uno slicing di un vettore di cui vogliamo parlare è quello mediante vettori logici. L’utilizzo di indicatori logici true e false è particolarmente efficace quando si lavora con istruzioni condizionali. Ad esempio, supponiamo di voler sapere se gli elementi di una matrice \(A\) sono maggiori degli elementi corrispondenti di un’altra matrice \(B\). L’operatore di confronto applicato alle due matrici restituisce un array logico i cui elementi sono 1 quando un elemento in \(A\) soddisfa il confronto con il corrispondente elemento in \(B\).

A = [1 2 6; 4 3 6];
B = [0 3 7; 3 7 5];
ind = A>B
A(ind)
B(ind)

ci restituisce

ind =

  2×3 logical array

   1   0   0
   1   0   1


ans =

     1
     4
     6


ans =

     0
     3
     5

Gli operatori di confronto non sono gli unici per cui è possibile compiere questa operazione, MATLAB stesso implementa un certo numero di funzioni utili a questo scopo, si vedano isnan, isfinite, isinf, ismissing. È inoltre possibile combinare insieme diverse richieste mediante l’uso degli operatori logici, si veda più avanti la sezione su Selezione e Strutture Condizionali.

Operazioni tra array e matrici

MATLAB supporta tutte le operazioni che hanno senso in termini di algebra lineare, dunque prodotti matrici-vettore, somme di matrici e di vettori, trasposizione, coniugio, etc., con i medesimi vincoli di consistenza tra gli operatori. Specificamente, il prodotto \(A \mathbf{v}\) con \(A \in \mathbb{R}^{n \times k_1}\) e \(\mathbf{v} \in \mathbb{R}^{k_2}\) è possibile se e solo se \(k_1 \equiv k_2\), consideriamo ad esempio

A = [1 2 3 4;
     4 3 2 1;
     2 4 3 1;
     3 2 4 1];
v1 = [1,2,3,4];
v2 = [1;2;3;4];

e proviamo a calcolare

• A*v1 da cui otteniamo un errore:

Error using  *
Incorrect dimensions for matrix multiplication. Check that the number of columns in the first matrix matches the number of rows in the second matrix. To perform elementwise multiplication, use '.*'.

poiché stiamo cercando di fare un’operazione che non ha senso dal punto di vista dell’algebra lineare.

• A*v2 è invece l’operazione corretta e otteniamo

ans =

    30
    20
    23
    23

• v1*A anche questa operazione ha senso dal punto di vista matriciale e infatti otteniamo

ans =

    27    28    32    13

• v2*A ha il medesimo problema della prima, cioè abbiamo di nuovo delle dimensioni che non sono consistenti

Error using  *
Incorrect dimensions for matrix multiplication. Check that the number of columns in the first matrix matches the number of rows in the second matrix. To perform elementwise multiplication, use '.*'.

• A*v1' introduciamo qui l’operazione di trasposta-coniugata (che poiché stiamo utilizzando vettori di numeri reali coincide con la semplice operazione di trasposizione .'), che ci porta ad avere le dimensioni corrette e ci restituisce

ans =

    30
    20
    23
    23

• A*v2' la trasposizione in questo caso rende le dimensioni di v2 incompatibili per cui otteniamo di nuovo il medesimo errore

Error using  *
Incorrect dimensions for matrix multiplication. Check that the number of columns in the first matrix matches the number of rows in the second matrix. To perform elementwise multiplication, use '.*'.

Avvertimento

Il messaggio di errore che abbiamo incontrato ci dice che l’operazione non ha senso in termine delle usuali operazioni dell’algebra lineare, tuttavia ci suggerisce che quello che potevamo avere intenzione di fare era un prodotto elementwise ovvero «elemento ad elemento». Questa operazione si ottiene utilizzando l’operatore .*, cioè con un . prefisso davanti all’operatore di prodotto che in genere significa proprio «esegui in maniera elemento-ad-elemento». Proviamo con la prima operazione sbagliata che abbiamo proposto:

A.*v1

che ci restituisce

ans =

     1     4     9    16
     4     6     6     4
     2     8     9     4
     3     4    12     4

Che operazione abbiamo eseguito? Si provi ad eseguire anche le operazioni di elevamento a potenza

A^3
A.^3
v1^3
v1.^3

e si descriva il risultato.

Le ultime due operazioni che ci sono rimaste da descrivere sono +/-. Di nuovo dobbiamo preoccuparci della compatibilità delle operazioni che vogliamo compiere. Se vogliamo essere sicuri di star eseguendo la somma tra array e matrici che abbiamo in mente dobbiamo assicurarci che le dimensioni siano compatibili.

Supponiamo di avere i vettori riga e colonna

v = [1 2 3 4]
w = [1
     2
     3
     4]

se vogliamo sommarli o sottrarli e ottenere un vettore rispettivamente riga o colonna dobbiamo fare in modo che abbiano ambedue la dimensione corretta. Ovvero, dobbiamo avere, rispettivamente,

v + w'

oppure

v' + w

Se inavvertitamente sommiamo i due vettori come

v + w

otteniamo invece

ans =

     2     3     4     5
     3     4     5     6
     4     5     6     7
     5     6     7     8

che è invece una matrice! Non esattamente quello che ci aspettavamo (riuscite a capire che operazione abbiamo ottenuto?). Uguale cautela va esercitata nello scrivere operazioni di somma/sottrazioni tra matrici e vettori. Si provi ad eseguire:

A = pascal(4);
v = [1 3 2 4];
A + v
A + v'
A + 0.5
v + 1

È legittimo domandarsi a questo punto perché mai queste operazioni vengano eseguite senza restituire errori. Anche se dal punto di vista della pura algebra lineare queste operazioni non sono di immediata sensatezza, dal punto di vista implementativo permettono di semplificare (e velocizzare) un certo numero di operazioni che altrimenti richiederebbero diverse righe di codice (la cui ottimizzazione per le performance non è scontata) per essere implementate.

Selezione e Strutture Condizionali

Tabella 3 Strutture Condizionali.

Funzione di MATLAB	Descrizione
if, elseif, else	Esegue comando se la condizione if è verificata
switch, case, otherwise	Esegue uno o più gruppi di comandi a seconda che la variabile switch abbia il valore indicato nel case, altrimenti esegue il comando o gruppo di comandi identificati da otherwise
try, catch	Esegue i comandi nel gruppo try, se questi restituiscono errore non blocca l’esecuzione e passa ai comandi racolti in catch

Consideriamo il seguente esempio che simula il lancio di una moneta.

a = rand();
if a < 0.5
  disp('Testa!')
else
  disp('Croce')
end

Ad ogni nuova esecuzione rand() genera un numero casuale in \([0,1]\) con probabilità uniforme. Il comando if controlla se il numero casuale generato è \(< 0.5\) ed in questo caso entra nel primo gruppo di codice. Altrimenti, abbiamo ottenuto un numero \(> 0.5\) e rientriamo nel secondo gruppo di codice. Possiamo decidere di simulare anche un dado a tre facce nel seguente modo

a = rand();
if a < 1/3
  disp('1')
elseif a >= 1/3 & a < 2/3
  disp('2')
else
  disp('3')
end

in cui abbiamo utilizzato il comando elseif per avere un ramo aggiuntivo.

Nota

All’interno dei nostri controlli di tipo if (e più in generale) possiamo combinare insieme il risultato di diverse operazioni logiche. Queste sono raccolte nella Tabella Tabella 4. Altre funzioni che agiscono sui vettori di logici e che potete esplorare richiamando la funzione help sono any e all.

Tabella 4 Operazioni logiche

Funzione di MATLAB	Descrizione
&	AND Logico
~	NOT Logico
|	OR Logico
xor	OR Esclusivo Logico

Vediamo anche un esempio dell’istruzione di tipo switch.

controllo = input("Inserisci un numero intero tra 0 e 3: ");
switch controllo
case 0
 A = pascal(4,4);
 disp(A);
case 1
 A = ones(4,4);
 disp(A);
case 2
 A = eye(4,4);
 disp(A);
case 3
 A = rand(4,4);
 disp(A);
otherwise
 disp("Non so cosa fare con questo input!")
end

Si sarebbe potuto implementare lo stesso codice con una serie di if e elseif ed un else, ma questo approccio è più rapido se non c’è la necessità di imporre molti controlli logici.

L’ultimo controllo che vogliamo testare è try. Per cui potete provare il seguente codice.

try
 A = rand(5,5);
 b = ones(1,5);
 A*b
catch
 disp("C'è qualche problema con le dimensioni!");
end

Poiché l’operazione algebrica che abbiamo richiesto non è ben posta (provate ad eseguirla al di fuori dell’operazione di try) il try cattura l’errore e invece di arrestare l’esecuzione esegue il codice nella clausola catch. Potete correggere il codice nel primo blocco e verificare che in tal caso non entrerete nel catch.

Cicli e Cicli Innestati

All’interno di qualsiasi programma, è possibile definire sezioni di codice che si ripetono in un ciclo.

Tabella 5 Strutture Condizionali.

Funzione di MATLAB	Descrizione
for	ciclo for per ripetere delle istruzioni un numero prefissato di volte
while	ciclo while ripete il suo codice fintanto che la condizione è true
break	Termina in maniera forzata l’esecuzione di un ciclo for o while
continue	Passa il controllo all’iterata successiva di un ciclo for o while
pause	Mette temporaneamente in pausa l’esecuzione di MATLAB.

Funzioni di stampa

MATLAB fornisce un porting abbastanza trasparente delle funzioni di stampa a schermo (su stream di dati) del C. Ovvero la funzione fprintf. Per la stampa a schermo il prototipo di questa funzione è

fprintf(FORMAT, A, ...)

dove FORMAT è una stringa che contiene informazioni sul formato da stampare e A è un array che contiene i dati che devono essere stampati secondo il formato FORMAT. In generale questo è una stringa che può contenere del testo accompagnato da dei caratteri di escape che dicono come formattare il dato contenuto nella variabile A. Come descritto nell’immagine l”escape per un operatore di formattazione comincia con il segno di percentuale, %, e finisce con un carattere di conversione (Tabella 6). Il carattere di conversione è richiesto. In maniera opzionale, si possono specificare un identificatore, delle flag, l’ampiezza del campo, la precisione, e un operatore di sottotipo tra il % ed il carattere di conversione.

Tabella 6 Caratteri di conversione

Carattere	Conversione
%d o %i	Intero base 10
%f	Floating point a precisione fissa
%e	Floating point notazione scientifica
%c	Singolo carattere
%s	Stringa

Un esempio:

fprintf("%f \n",pi);
fprintf("%e \n",5*10^20);
fprintf("%1.2f \n",pi);
fprintf("%1.2e \n",5*10^20);
fprintf("%c \n",'a')
fprintf("%s \n",'Ciao, mondo!')

Nell’esempio abbiamo usato ripetutamente i caratteri \n che stanno a simboleggiare un carattere di fine linea. Altri caratteri utili di questo tipo sono in Tabella 7.

Tabella 7 Caratteri di formattazione

Risultato	Stringa
Singolo quotation mark	''
Simbolo percento	%%
Backslash	\\
Backspace	\b
Tab orizzontale	\t
Tab verticale	\v

Ulteriori informazioni possono essere ottenuto scrivendo help fprintf nella command line.

Utilizziamo un ciclo for per calcolare la somma dei primi n numeri interi.

n = input("Inserisci un numero intero n: ");
somma = 0;
for i=1:n
  somma = somma + i;
end
fprintf("La somma degli interi da 1 a %d è %d.\n",n,somma);

Questo non è ovviamente il modo migliore di fare questa operazione, avremmo ad esempio potuto calcolare la stessa quantità come sum(1:10). Oppure, sfruttare un po” di idee matematiche per ricordarci che \(\displaystyle S_n = \sum_{i=1}^{n} i = \frac{n(n+1)}{2}.\) Ma è servito al nostro scopo dimostrativo.

Vediamo ora un esempio di ciclo while.

somma = 0;
while somma < 10
  somma = somma + rand();
end
fprintf("Il valore finale della somma è: %f\n",somma);

Poiché abbiamo inizializzato la variabile somma a 0, la condizione di innesco del ciclo while è true e dunque cominciamo ad iterare. Ad ogni nuova istanza del ciclo un nuovo numero casuale viene generato e aggiunto alla variabile somma. Non appena il valore di somma supera 10, il ciclo viene interrotto e il messaggio viene stampato a schermo.

Alcuni esercizi

Gli esercizi qui raccolti hanno per lo più lo scopo di verificare che abbiate assorbito queste informazioni generali sul linguaggio MATLAB, cosicché dal prossimo laboratorio ci si possa concentrare sull’implementazione di algoritmi prettamente numerici e sulle questioni affrontate nelle lezioni di teoria.

Esercizio 1

Scrivere una funzioni che calcoli la norma \(L^p\) di un vettore, definita come

\[ \|v \|_{\ell^p} := \left(\sum_i |v_i|^p\right)^{1/p} \]

se \(p\neq\infty\), altrimenti

\[ \|v \|_{\ell^\infty} := \max_{i} |v_i| \]

La funzione dovrebbe prendere come argomenti vettore di \(R^d\), e un numero \(p\) nell’intervallo \([1, \infty]\), che indica l’esponente della norma. Nota: \(\infty\) in matlab si indica con Inf.

Scrivere un errore se l’esponente non è nell’intervallo atteso.

function [norm] = lp_norm(v, p)
%% Calcola la norma l_p del vettore v, con esponente p
% qui il tuo codice
end

Esercizio 2

In questo esercizio dovrai capire quali sono i valori ottimali dell’intervallo di passo quando si approssimano le derivate utilizzando il metodo delle differenze finite.

Scrivi un programma per calcolare l’approssimazione della differenza finita (FD) della derivata di una funzione f, calcolata al punto x, utilizzando un passo di dimensione h. Ricorda la definizione di derivata approssimata:

\[ fd(f,x,h) := \frac{f(x+h)-f(x)}{h} \]

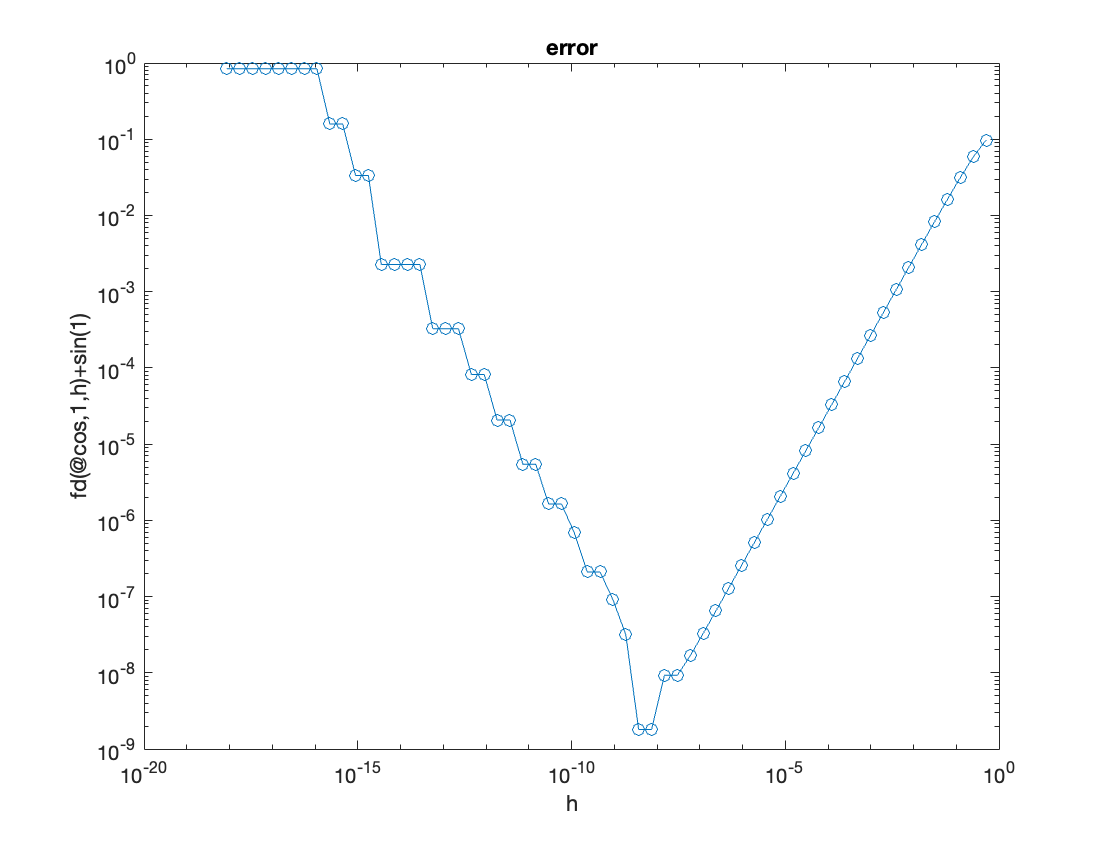
Applica questo metodo alla funzione cos, calcolane la derivata approssimata in 1, e confronta il tuo risultato con la soluzione esatta -sin(1). Ripeti il procedimento per h in \(2^{-i}\) con \(i\) che varia tra 1 e 60, e salva l’errore in un vettore.

Plotta il risultato (in scala logaritmica), e commenta quello che osservi. Dovresti ottenere qualcosa di simile a

Nota: se si vuole passare una funzione come argomento ad un altra funzione, si possono usare le function handle, ovvero il simbolo @. Consideriamo per esempio la seguente funzione, che si aspetta di poter chiamare il suo primo argomento come se fosse una funzione:

function [res] = use_function(f,x)
res = f(x);
end

per poter usare use_function passando come argomento una funzione già definita, ad esempio la funzione cos, devo scrivere:

res = use_function(@cos, x);
% equivalente a scrivere: res = cos(x);

La «function handle», può essere usata anche per definire funzioni «al volo», ad esempio:

res = use_function(@(x) x^2, x);

la scrittura f = @(x) x^2 è equivalente a definire una funzione

function res = f(x)
res = x^2
end

ovvero:

f = @(x) x^2

f =

  function_handle with value:

    @(x)x^2
 
>> f(2)

ans =

     4

Grafici

Per disegnare un grafico con Matlab, si utilizza la funzione plot.

La funzione plot prende come argomenti le coordinate x e y dei punti da tracciare sul grafico. Ad esempio, per disegnare un grafico di una funzione lineare, si possono fornire due vettori di coordinate x e y, dove x rappresenta i valori sull’asse x e y rappresenta i valori sull’asse y corrispondenti.

Ecco un esempio di utilizzo della funzione plot:

x = linspace(0,2*pi,100);
y = cos(x);
plot(x,y);

che produce il seguente grafico:

Per fare il grafico degli errori, è spesso utile farlo in scala logaritmica o semilogaritmica. Ciò si ottiene con i comandi semilogx, semilogy, loglog, che funzionano in modo simile al comando plot.

Esercizio 3

La costante aurea \(\varphi\) si può esprimere in forma compatta come

\[\varphi = \frac{1+\sqrt{5}}{2}.\]

Ammettiamo di non avere un algoritmo per estrarre le radici quadrate, allora possiamo provare ad approssimare il valore di \(\phi\) usando la sua espansione in frazione continua:

\[\varphi = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \vdots } } } } } }\]

Si scriva una funzione con il seguente prototipo:

function phi = frazionephi(n)
%%FRAZIONEPHI prende in input il numero di termini da utilizzare
%nell'approssimazione con frazione continua della sezione aurea e
%restituisce l'approssimazione.
end

• Per costruire l’implementazione della funzione si usi un ciclo for. Suggerimento si organizzi il calcolo partendo dal «livello più basso» verso quello più alto.

• Supponiamo di sapere che un valore esatto di \(\varphi\) con 16 cifre significative è 1.6180339887498949. Si modifichi la funzione precedente in una nuova funzione con il seguente prototipo

  function [n,phi] = quantiterminiphi(tol)
  %%QUANTITERMINIPHI data in input una tolleranza tol sulla distanza tra
  %l'approssimazione della costante phi e il valore reale questa funzione
  %ci restituisce il numero di termini necessari e il valore dell'approssimazione
  
  phitrue = 1.6180339887498949;
  
  end
  

  Per farlo si usi un ciclo while e la funzione abs (che implementa il valore assoluto) per misurare l”errore assoluto tra la nostra approssimazione e il valore vero.

• Si usi la funzione fprintf per stampare a schermo una tabella con tolleranza, numero di termini per raggiungerla, valore ottenuto ed errore per le tolleranze da 1e-1, 1e-2, fino a 1e-10.

Esercizio 4

Esercitiamoci ora nel costruire una funzione ricorsiva. Una sequenza collegata alla costante aurea \(\varphi\) è la sequenza di Fibonacci, ovvero la sequenza di numeri interi \(\{F_n\}_n = \{1,1,2,3,5,\ldots\}\) data da

\[F_{n+1} = F_{n} + F_{n-1}, \text{ se } n \geq 1, \; F_{1} = 1,\;F_{0} = 1.\]

• Si implementi una funzione ricorsiva che calcola l”\(n\)mo numero di Fibonacci \(n\) utilizzando solamente la struttura condizionale switch, di cui riportiamo al solito il prototipo.

function f = fibonacci(n)
%FIBONACCI Implementazione ricorsiva della successione di Fibonacci. Prende
%in input il numero n e restituisce l'n-mo numero di Fibonacci Fn.
end

• La funzione così costruita ha uno spiacevole difetto, se gli diamo in pasto \(n\) ci fornisce l”\(n\)mo numero, tuttavia se successivamente chiediamo l”\(n+1\)mo il calcolo per ottenerlo non ha memoria di quello che abbiamo fatto e ricalcola comunque tutti i precedenti. Costruiamo ora una versione non ricorsiva della funzione fibonacci. Possiamo ottenerla in diversi modi, ma quasi sicuramente avremo bisogno di un ciclo for. Riportiamo come al solito il prototipo.

function f = fibonaccinonrecursive(n)
%FIBONACCINONRECURSIVE Implementazione non ricorsiva della successione
% di Fibonacci. Prende in input il numero n e restituisce un vettore
% che contiene tutti i numeri di Fibonacci da F0 a Fn.
end

• Sfruttiamo ora la seconda implementazione che abbiamo fatto della funzione di Fibonacci per costruire una sequenza diversa. Consideriamo la sequenza di Viswanath [Vis00] così definita

\[v_{n+1} = v_{n} \pm v_{n-1}, \; n \geq 1,\]

dove \(v_{0}\) e \(V_{1}\) sono assegnati a piacere e il \(\pm\) ha la seguente interpretazione: con probabilità \(1/2\) sommiamo, con probabilità \(1/2\) sottraiamo. Un’idea per implementare questa funzione è quella di utilizzare la funzione sign (provate a vedere a cosa serve facendo help sign). Un prototipo per questa funzione è ad esempio

function v = viswanath(n,v0,v1)
%VISWANATH Implementazione non ricorsiva della successione
% di Viswanath. Prende in input il numero n, i valori di v0 e v1 e
% restituisce un vettore che contiene tutti i numeri di Viswanath da v0 a vn.
end

• Una volta costruita la nostra funzione, possiamo visualizzare cosa otteniamo con essa (e confrontarlo con la successione di Fibonacci) tramite lo script:

%% Test della successione di Viswanath

n = 1000; % Numero di termini

% Calcoliamo la successione di Fibonacci
f = fibonaccinonrecursive(n);

% Calcoliamo la successione di Viswanath
v0 = 1;
v1 = 1;
v = viswanath(n,v0,v1);

% Valore asintotico
c = 1.13198824;
phi = (1+sqrt(5))/2;
figure(1)
semilogy(0:n,abs(v),'o',0:n,c.^(1:n+1),'-',0:n,f,'x',0:n,phi.^(1:n+1),'-');
legend({'Viswanath','Stima Asintotica','Fibonacci','Stima Asintotica'},...
    'Location','northwest')

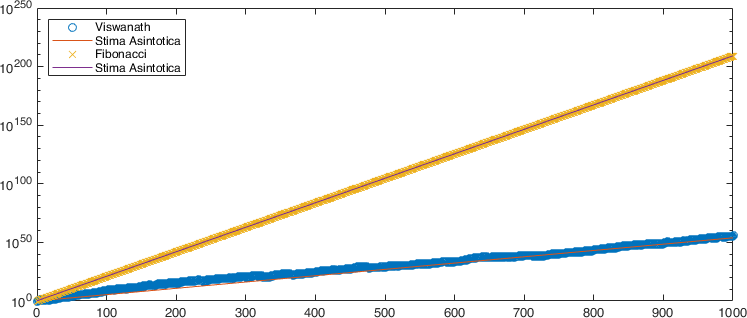
Nella parte terminale dello script % Valore asintotico andiamo a confrontare in scala semi-logaritmica sull’asse delle \(y\) i valori assoluti dei numeri \(\{v_n\}_n\) e gli \(\{F_n\}_n\). In particolare possiamo osservare che per entrambe le sequenza troviamo un numero \(k\) per cui queste crescono come \(k^{n+1}\). In particolare, per la sequenza di Fibonacci questo \(k\) è la costante aurea \(\varphi\) dell’esercizio precedente, mentre per la sequenza di Viswanath è il valore \(c = 1.13198824\ldots\) (per una dimostrazione si veda [Vis00]).

Approfittiamo di questo anche per guarda come si possono ottenere dei grafici di funzione su MATLAB, per decodificare i comandi di questa sezione aiutatevi con help. Un esempio del grafico ottenuto con lo script precedente è il seguente:

Insieme di Mandelbrot

Esercizio 5

Esploriamo ancora le funzioni di plot di MATLAB. Cerchiamo di produrre una stampa dell’insieme frattale di Mandelbrot. Questo insieme è l’insieme è l’insieme dei numeri complessi \(c\) per cui la funzione \(f_{c}(z)=z^{2}+c\) non diverge quando viene iterata a partire da \(z = 0\), cioè, l’insieme di quei punti \(c\) per cui la sequenza \(f_{c}(0),f_{c}(f_{c}(0)),\ldots\) resta limitata in valore assoluto. Possiamo costruire uno script MATLAB che ci permetta di disegnare un’approssimazione di questo insieme.

1. Utilizziamo la funzione linspace per costruire l’insieme dei numeri complessi \(c\) su cui vogliamo fare la valutazione. Poiché linspace produce per noi un vettore reali, dobbiamo costruirne due – uno per ciascuna direzione – e trasformarli in un insieme di coppie di valutazioni con la funzione meshgrid. Un buon insieme reale da valutare per disegnare l’insieme di Mandelbrot è \([-2.1,0.6]\times[-1.1,1.1]\).

2. Ora che abbiamo le valutazioni reali è necessario trasformare in numeri complessi \(c\). Possiamo ottenere questo risultato utilizzando la funzione complex: C = complex(X,Y) sulla coppia di matrici di valutazioni ottenute da meshgrid.

3. Possiamo ora implementare un certo numero fissato di iterazioni della funzione \(f_{c}(z)=z^{2}+c\) mediante un ciclo for.

4. Concludiamo l’esercizio disegnando l’insieme di Mandelbrot con la funzione

contourf(x,y,double(abs(Z)<1e6))
title('Insieme di Mandelbrot')

che è una buona occasione per guardare cosa fa la funzione di plot contourf (help contourf).

Bibliografia

Vis00(1,2)

Divakar Viswanath. Random Fibonacci sequences and the number $1.13198824…$. Math. Comp., 69(231):1131–1155, 2000. URL: https://doi.org/10.1090/S0025-5718-99-01145-X, doi:10.1090/S0025-5718-99-01145-X.