Laboratorio 9 : Metodi Iterativi Stazionari per Sistemi Lineari#

Un metodo iterativo è una procedura matematica che a partire da un valore iniziale genera una sequenza di soluzioni approssimate migliorative, in cui l’approssimazione \(n\)-esima è derivata dalle precedenti.

In questo laboratorio vogliamo concentrarci sulla costruzione di alcuni metodi di questo tipo per la soluzione di sistemi lineari.

La prima domanda che è legittimo porsi è perché mai vogliamo mettere in piedi dei metodi iterativi se abbiamo già dei metodi diretti che possono raggiungere la soluzione del problema cercato?

  • A patto di richiedere una tolleranza minore (spesso sufficiente nelle applicazioni) sull’errore commesso sulla soluzione hanno un costo computazionale inferiore alle controparti dirette.

  • Per le dimensioni dei problemi che si vogliono affrontare nelle applicazioni ingegneristiche attuali sono spesso l’unica opzione disponibile (problemi di fluidodinamica computazionale, combustione, meccanica del continuo, …).

Metodi di tipo stazionario#

Dato un sistema lineare della forma

\[A \mathbf{x} = \mathbf{b}, \qquad A \in \mathbb{R}^{n \times n},\; \mathbf{x},\mathbf{b} \in \mathbb{R}^n\]

siamo interessati a metodi di punto fisso basati su una decomposizione additiva della matrice \(A\) della forma

\[A = M - N, \qquad\text{ con }\qquad \det(M) \neq 0.\]

Da questa decomposizione si ottiene poi l’iterata di punto fisso come

\[\begin{split}A \mathbf{x} = \mathbf{b} \Rightarrow (M - N) \mathbf{x} = \mathbf{b} \Rightarrow M \mathbf{x} = N \mathbf{x} + \mathbf{b} \\ \mathbf{x} = M^{-1} N \mathbf{x} + M^{-1} \mathbf{b}\end{split}\]

e quindi

\[\begin{split}\mathbf{x}^{(k+1)} = M^{-1} N \mathbf{x}^{(k)} + M^{-1} \mathbf{b}, \quad k = 0,1,2,\ldots, \\ \mathbf{x}^{(0)} \text{ assegnato}.\end{split}\]

Essendo questa un’iterata di punto fisso, la sua convergenza dipende dall’essere una procedura contrattiva, avete dimostrato a lezione che questo è equivalente alla richiesta che il raggio spettrale della matrice di iterazione \(M^{-1}N\) sia strettamente minore di \(1\):

\[\rho(M^{-1}N) = \max_{i=1,\ldots,n}|\lambda_i(M^{-1}N)| < 1.\]

Metodo di Jacobi#

Il primo metodo che vogliamo implementare è il metodo di Jacobi, questo è basato sullo splitting additivo per la matrice \(A\) con \(A = D - N\) dove \(D\) è la diagonale della matrice \(A\).

Teorema

Una condizione sufficiente (ma non necessaria) affinché il metodo di Jacobi sia convergente è che la matrice \(A\) sia a diagonale strettamente dominante, oppure a diagonale dominante e irriducibile.

Per trasformare il metodo in qualcosa di applicabile dobbiamo accoppiarlo ad un criterio d’arresto. Come sempre possiamo guardare al residuo assoluto oppure a quello relativo in una norma prefissata. Poiché abbiamo deciso di guardare alla convergenza attraverso informazioni spettrali scelta più naturale (e predittiva) è quella di usare la norma \(\|\cdot\|_ 2\).

\[\|\mathbf{r}^{(k)}\|_2 = \| A \mathbf{x}^{(k)} - \mathbf{b}\|_2 \leq \varepsilon,\]

ovvero, rispettivamente

\[\|\mathbf{r}^{(k)}\|_2 = \| A \mathbf{x}^{(k)} - \mathbf{b}\|_2 \leq \varepsilon \|\mathbf{r}^{(0)}\|_2,\]

dove \(\varepsilon\) è una tolleranza prefissata.

Esercizio

Si scriva una function che implementi il metodo di Jacobi per la soluzione di un sistema lineare \(A \mathbf{x} = \mathbf{y}\) entro una tolleranza \(\varepsilon\) sfruttando il seguente prototipo:

function [x,res,it] = jacobi(A,b,x,itmax,eps)
%%JACOBI implementa il metodo di Jacobi per la soluzione del sistema A x = b
%    INPUT:
%     A matrice quadrata
%     b termine destro del sistema lineare da risolvere
%     x innesco della strategia iterativa
%     itmax massimo numero di iterazioni lineari consentito
%    OUTPUT
%     x ultima soluzione calcolata dal metodo
%     res vettore dei residui
%     it numero di iterazioni
end

  • Si implementi in maniera vettoriale, cioè senza usare cicli for per scorrere le righe della matrice.

  • Si usi il criterio d’arresto basato sull’errore relativo.

Per testare il metodo si usi il seguente programma

A = gallery('poisson',10); % Matrice di prova
b = ones(10^2,1);           % rhs vettore di 1
x = zeros(10^2,1);          % Tentativo iniziale vettore di 0
[x,res,it] = jacobi(A,b,x,1000,1e-6);

figure(1)
semilogy(1:it,res,'o-','LineWidth',2);
xlabel('Iterazione');
ylabel('Residuo relativo');

Metodo di Gauss-Seidel#

Il secondo metodo di questo tipo che avete visto è il metodo di Gauss-Seidel, per questo metodo la decomposizione additiva della matrice \(A\) è \(A = L - N\), dove \(L\) è la parte triangolare inferiore della matrice \(A\).

Teorema

Una condizione sufficiente (ma non necessaria) affinché il metodo di Gauss-Seidel sia convergente è che la matrice \(A\) sia a diagonale strettamente dominante, oppure una matrice simmetrica e definita positiva.

Possiamo sfruttare di nuovo il residuo relativo per definire il criterio d’arresto.

Esercizio

Si scriva una function che implementi il metodo di Gauss-Seidel in avanti per la soluzione di un sistema lineare \(A \mathbf{x} = \mathbf{y}\) entro una tolleranza \(\varepsilon\) sfruttando il seguente prototipo:

function [x,res,it] = forwardgs(A,b,x,itmax,eps)
%%FORWARDGS implementa il metodo di Gauss-Seidel in avanti per la soluzione del
% sistema A x = b
%    INPUT:
%     A matrice quadrata
%     b termine destro del sistema lineare da risolvere
%     x innesco della strategia iterativa
%     itmax massimo numero di iterazioni lineari consentito
%    OUTPUT
%     x ultima soluzione calcolata dal metodo
%     res vettore dei residui
%     it numero di iterazioni
end

  • Si implementi in maniera vettoriale, cioè senza usare cicli for per scorrere le righe della matrice.

  • Si utilizzi la funzione forwardsolve vista in Sostituzione in avanti e all’indietro.

  • Si usi il criterio d’arresto basato sull’errore relativo.

Per testare il metodo si usi il seguente programma

A = gallery('poisson',10); % Matrice di prova
b = ones(10^2,1);           % rhs vettore di 1
x = zeros(10^2,1);          % Tentativo iniziale vettore di 0
[x,res,it] = forwardgs(A,b,x,1000,1e-6);

figure(1)
semilogy(1:it,res,'o-','LineWidth',2);
xlabel('Iterazione');
ylabel('Residuo relativo');

Paragone tra i due metodi e velocità di convergenza#

Adesso che abbiamo implementato i due diversi metodi possiamo fare un confronto delle loro prestazioni. Possiamo paragonare in primo luogo le due storie di convergenza guardando all’evoluzione dei residui:

A = gallery('poisson',10); % Matrice di prova
b = ones(10^2,1);           % rhs vettore di 1
x = zeros(10^2,1);          % Tentativo iniziale vettore di 0

[xjacobi,resjacobi,itjacobi] = jacobi(A,b,x,1000,1e-6);
[xforwardgs,resforwardgs,itforwardgs] = forwardgs(A,b,x,1000,1e-6);


figure(1)
semilogy(1:itjacobi,resjacobi,'o-',...
    1:itforwardgs,resforwardgs,'x-', 'LineWidth',2);
xlabel('Iterazione');
ylabel('Residuo');
legend({'Jacobi','Gauss-Seidel (Forward)'},...
    'Location','northeast',...
    'FontSize',14);

Da cui osserviamo che il metodo di Gauss-Seidel (forward) impiega meno iterazioni per raggiungere la convergenza desiderata (Fig. 9).

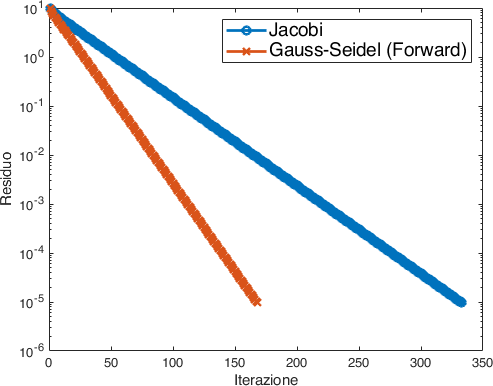
convergenza-metodi

Fig. 9 Evoluzione del residuo per i metodi di Jacobi e Gauss-Seidel.#

Possiamo indagare la cosa dal punto di vista teorico andando a guardare il raggio spettrale delle due matrici di iterazione, infatti

M = diag(diag(A)); % Jacobi
N = M - A;
rhojacobi = eigs(N,M,1,'largestabs');

M = tril(A); % Gauss-Seidel (forward)
N = M - A;
rhoforwardgs = eigs(N,M,1,'largestabs');

fprintf('Il raggio spettrale per Jacobi è %f\n',abs(rhojacobi));
fprintf('Il raggio spettrale per Gauss-Seidel è %f\n',abs(rhoforwardgs));

Da cui scopriamo che:

Il raggio spettrale per Jacobi è 0.959493
Il raggio spettrale per Gauss-Seidel è 0.920627

dunque Gauss-Seidel (forward) ha un tasso di riduzione del residuo minore e una convergenza più rapida.

Possiamo aggiungere delle istruzioni tic e toc per valutare anche il tempo impiegato dai due differenti metodi:

Il tempo per Jacobi è 0.008983 s
Il tempo per Gauss-Seidel è 0.182575 s

ovvero il metodo di Jacobi è in questo caso circa due ordini di grandezza più rapido. Tuttavia, se andiamo a sostituire la nostra implementazione della funzione forwardsolve con il \ implementato da MATLAB scopriamo che:

Il tempo per Jacobi è 0.008191 s
Il tempo per Gauss-Seidel è 0.004435 s

ed ora Gauss-Seidel ha ampiamente recuperato su Jacobi. L”implementazione conta! Qui il vantaggio è dato dal fatto che la matrice \(L\) associata al problema di test che stiamo guardando è una matrice a banda i non-zeri non riempiono tutto il triangolo. Il codice di MATLAB è in grado di accorgersene e adatto l’algoritmo di soluzione in modo che se ne tenga conto.