Laboratorio 7a : Soluzione di Sistemi Lineari Triangolari#

In questo e nel prossimo laboratorio ci focalizzeremo sul problema di risolvere un sistema lineare compatibile. Partiremo dal caso dei sistemi triangolari per poi occuparci, nel Laboratorio 7b, del caso generale tramite la fattorizzazione \(PA = LU\) della matrice dei coefficienti.

Soluzione di sistemi triangolari#

I sistemi triangolari giocano un ruolo fondamentale nei calcoli matriciali. Molti metodi sono costruiti sull’idea di ridurre un problema alla soluzione di uno o più sistemi triangolari, questo include praticamente tutti i metodi diretti per la risoluzione di sistemi lineari.

Due funzioni utili per lavorare con i sistemi triangolari sono le funzioni triu e tril. Dal loro help:

tril Extract lower triangular part.
   tril(X) is the lower triangular part of X.
   tril(X,K) is the elements on and below the K-th diagonal
   of X .  K = 0 is the main diagonal, K > 0 is above the
   main diagonal and K < 0 is below the main diagonal.

ed analogamente per triu:

triu Extract upper triangular part.
   triu(X) is the upper triangular part of X.
   triu(X,K) is the elements on and above the K-th diagonal of
   X.  K = 0 is the main diagonal, K > 0 is above the main
   diagonal and K < 0 is below the main diagonal.

Possiamo usarle per costruire sistemi triangolari a partire da sistemi densi.

Sostituzione in avanti e all’indietro#

Sui computer seriali i sistemi triangolari sono universalmente risolti dagli algoritmi standard di sostituzione in avanti e all’indietro. Sulle macchine parallele la situazione è sensibilmente più varia, ma questo trascende gli obiettivi di questo corso.

Sia \(L\) una matrice triangolare inferiore, vogliamo risolvere un sistema della forma:

\[L \mathbf{x} = \mathbf{b},\]

che possiamo riscrivere in forma estesa come:

\[\begin{split}\begin{bmatrix} l_{1,1} & 0 & 0 & \cdots & 0 \\ l_{2,1} & l_{2,2} & 0 & \cdots & 0 \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ l_{n-1,1} & l_{n-1,2} & \cdots & l_{n-1,n} & 0 \\ l_{n,1} & l_{n,2} & \cdots & \cdots & l_{n,n} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_{n-1}\\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_{n-1} \\ b_n \end{bmatrix}\end{split}\]

Da cui è facile ricavare che la componente \(i\)ma della soluzione è

\[x_i = \frac{1}{l_{i,i}} \left( b_i - \sum_{j=1}^{i-1} l_{i,j} x_j \right), \qquad i=1,\ldots,n.\]

Esercizio 1

Si scriva una function che implementa il metodo di sostituzione in avanti con il seguente prototipo.

function [x] = forwardsolve(A,b)
% FORWARDSOLVE Se A è una matrice triangolare inferiore risolve
% il sistema Ax=b tramite metodo di sostituzione in avanti.
%   Input:
%   A = matrice triangolare inferiore
%   b = vettore del termine noto
%   Output:
%   x = vettore della soluzione

end

Si presti attenzione:

alla verifica degli input, il sistema deve essere triangolare inferiore e quadrato;
ad utilizzare le operazioni vettorizzate di MATLAB, ovvero si ragioni su come evitare di usare un ciclo for per effettuare la somma che compare nella formula di soluzione.

Si può testare il codice con il seguente problema:

%% Sostituzione in avanti
n = 10;
A = tril(ones(n,n));
b = (1:n).';
x = forwardsolve(A,b);

fprintf("Sostituzione in avanti: Errore sulla soluzione è: %1.2e\n",norm(A*x-b));

Sia \(U\) una matrice triangolare superiore, vogliamo risolvere un sistema della forma:

\[U \mathbf{x} = \mathbf{b},\]

che possiamo riscrivere in forma estesa come:

\[\begin{split}\begin{bmatrix} u_{1,1} & u_{1,2} & \cdots & \cdots & u_{1,n} \\ 0 & u_{2,2} & u_{2,3} & \cdots & u_{2,n} \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & u_{n-1,n-1} & u_{n-1,n} \\ 0 & 0 & \cdots & 0 & u_{n,n} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_{n-1}\\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_{n-1} \\ b_n \end{bmatrix}\end{split}\]

Da cui di nuovo ricaviamo facilmente la componente \(i\)ma della soluzione come:

\[x_i = \frac{1}{u_{i,i}} \left( b_i - \sum_{j=i+1}^{n} u_{i,j} x_j \right), \qquad i=n,n-1,\ldots,1.\]

Esercizio 2

Si scriva una function che implementa il metodo di sostituzione all’indietro con il seguente prototipo.

function [x] = backwardsolve(A,b)
% BACKWARDSOLVE Se A è una matrice triangolare superiore risolve
% il sistema Ax=b tramite metodo di sostituzione all'indietro.
%   Input:
%   A = matrice triangolare inferiore
%   b = vettore del termine noto
%   Output:
%   x = vettore della soluzione

end

Si presti attenzione:

alla verifica degli input, il sistema deve essere triangolare superiore e quadrato;
ad utilizzare le operazioni vettorizzate di MATLAB, ovvero si ragioni su come evitare di usare un ciclo for per effettuare la somma che compare nella formula di soluzione.

Si può testare il codice con il seguente problema:

%% Sostituzione all'indietro
n = 10;
A = triu(ones(n,n));
b = (1:n).';
x = backwardsolve(A,b);

fprintf("Indietro: Errore sulla soluzione è: %1.2e\n",norm(A*x-b));

Tempo di calcolo#

Si è visto a lezione che il numero di operazioni necessario a risolvere un sistema triangolare con l’algoritmo di sostituzione è un \(O(n^2)\) con \(n\) la dimensione del sistema. Proviamo ad indagare come si comporta a questo riguardo la nostra implementazione. Per farlo sfruttiamo i codici che abbiamo appena scritto per la sostituzione forward o backward e le funzioni tic e toc.

sizes = floor(logspace(1,4,10));
times = zeros(size(sizes));
h = waitbar(0,"Calcolo in corso...");
for i=1:length(sizes)
    n = sizes(i);
    A = triu(ones(n,n));
    b = (1:n).';
    tic;
    x = backwardsolve(A,b); % Allo stesso modo con forwardsolve
    times(i) = toc;
    waitbar(i/length(sizes));
end

Ora che abbiamo i tempi possiamo visualizzare quello che abbiamo ottenuto sfruttando alcune funzioni di MATLAB. Poiché sappiamo che il numero di operazioni è una funzione che scala come un \(O(n^2)\) possiamo assumere in prima approssimazione che anche il tempo si comporti allo stesso modo. Cerchiamo dunque di fittare un polinomio di secondo grado ai nostri dati:

[P,S] = polyfit(sizes,times,2);

Con la mia macchina, questa procedure mi restituisce il polinomio:

\[p(x) = 0.000005682501880 x^2 -0.015569138451058 x + 3.230452264767748\]

insieme ad una struttura \(S\) che contiene informazioni relative all’algoritmo con cui questa procedura è stata eseguita. Possiamo usare tutto questo per confrontare i valori del fit con quelli dei dati

[y_fit,delta] = polyval(P,sizes,S);
plot(sizes,times,'o-',...
    sizes,y_fit,'--',...
    sizes,y_fit+2*delta,'m--',sizes,y_fit-2*delta,'m--',...
    'Linewidth',2);
xlabel('Dimensione del sistema')
ylabel('Tempo di calcolo (s)')
legend({'Tempo misurato','Stima asintotica','Intervallo di Confidenza'},...
    'FontSize',14,'Location','northwest');

dove abbiamo stampato sia il tempo misurato, sia il fit con il suo intervallo di confidenza entro il 95%. Dalla Fig. 5 vediamo che la predizione quadratica è piuttosto efficace.

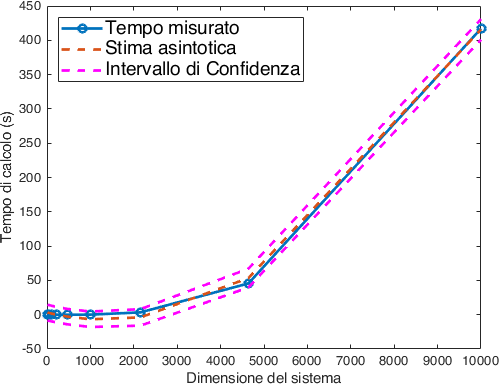
_images/triangulartime.png — Fig. 5 Tempo di calcolo come un \(O(n^2)\) della dimensione.#

Esercizi#

Esercizio 3: Numeri di Bernoulli

Consideriamo le condizioni

\[B(x+1) - B(x) = n x^{n-1}, \quad \int_{0}^{1} B(x)\,{\rm d}x, \quad B(x)\, \text{polinomio}.\]

Queste definiscono in maniera unica la funzione \(B(x)\). Se assumiamo che il grado del polinomio monico \(B(x)\) sia \(n\) abbiamo così costruito i polinomi di Bernoulli. Si possono calcolare esattamente i primi polinomi come:

\[B_0(x) = 1, \quad B_1(x) = x - \frac{1}{2}, \quad B_2(x) = x(x-1)+\frac{1}{6}, \quad B_3(x) = x(x-\frac{1}{2})(x-1), \ldots\]

Si può dimostrare che i polinomi di Bernoulli definiscono i coefficienti della rappresentazione in serie di potenze di diverse funzioni, ad esempio:

\[\frac{t e^{xt}}{e^t - 1} = \sum_{k=0}^{+\infty} \frac{B_n(x)}{n!}t^n.\]

In particolare, se scegliamo \(x = 0\), abbiamo che

(8)#\[\frac{t}{e^t - 1} = -\frac{1}{2}t + \sum_{k=0}^{+\infty} \frac{B_{2k}(0)}{(2k)!}t^{2k}.\]

Facciamo ora la seguente manipolazione algebrica, moltiplichiamo l’equazione a sinistra e a destra per \(e^{t} - 1\), espandiamo \(e^{t}\) con la sua serie di potenze, e poniamo uguale a zero i coefficienti di \(t^i\) sul lato destro. Così otteniamo il seguente sistema di equazioni:

\[- \frac{1}{2} j + \sum_{k=0}^{[\frac{j-1}{2}]} \binom{j}{2k} B_{2k}(0), \qquad j=2,3,4,\ldots\]

Da cui otteniamo, per gli \(j\) pari, il seguente sistema di equazioni lineari

\[\begin{split}\begin{bmatrix} \binom{2}{0} \\ \binom{4}{0} & \binom{4}{2} \\ \binom{6}{0} & \binom{6}{2} & \binom{6}{4} \\ \binom{8}{0} & \binom{8}{2} & \binom{8}{4} & \binom{8}{6} \\ \vdots & \vdots & \vdots & \vdots & \ddots \\ \end{bmatrix} \begin{bmatrix} B_0(0)\\ B_2(0)\\ B_4(0)\\ B_6(0)\\ \vdots \end{bmatrix} = \begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \vdots \end{bmatrix}.\end{split}\]

Si implementi una funzione che dato un intero \(k\) restituisca i numeri di Bernoulli \(\{B_{2j}(0)\}_{j=0}^{k}\) risolvendo questo sistema lineare.
Si usino i numeri così ottenuti per determinare lo sviluppo in (8) e disegnare

le due funzioni una accanto all’altra,
l’errore di approssimazione commesso in scala logaritmica.

Un prototipo della funzione è:

function [Bk] = nbernoulli(k)
% NBERNOULLI Produce i numeri di Bernoulli B_{2j}(0) per j=0,...,k
% risolvendo un sistema triangolare inferiore.
%   INPUT:
%   k =  Numero di termini (-1) da calcolare
%   OUTPUT:
%   Bk = Vettore di lunghezza k+1 che contiene i numeri richiesti
end

Suggerimento

La funzione binomiale in MATLAB è implementata come nchoosek. Potete inoltre confrontare i risultati ottenuti con la funzione nativa di MATLAB che calcola i numeri di Bernoulli dal medesimo nome (help bernoulli per le informazioni).

Calcolo Numerico - Esercitazioni di Laboratorio

Laboratorio 7a : Soluzione di Sistemi Lineari Triangolari

Contents