Laboratorio 10b : Il Metodo di Newton

Nello scorso laboratorio abbiamo affrontato il problema di trovare lo zero di una funzione continua \(f : \mathbb{R} \to \mathbb{R}\) utilizzando il metodo di bisezione. Il passo successivo visto a lezione è quello di costruire un metodo che, a patto di avere funzioni di regolarità più alta, \(f \in \mathcal{C}^{2}(\mathbb{R})\), permette di ottenere una velocità di convergenza maggiore.

Prima di dedicarci all’implementazione, riprendiamo brevemente l’idea e la costruzione del metodo. L’idea è di cominciare con una approssimazione iniziale che sia ragionevolmente vicina alla radice dell’equazione che vogliamo risolvere. Approssimiamo in quel punto la funzione con la tangente, calcoliamo la sua intercetta con l’asse delle \(x\) e quella è la nuova approssimazione per la radice. Possiamo iterare la procedura come:

(13)\[x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)}, \quad x_0 \text{ assegnato},  \quad k \geq 1,\]

Per cui avete dimostrato il seguente teorema di convergenza.

Teorema

Sia \(f \in \mathcal{C}^{2}([a,b])\), e supponiamo inoltre che \(f(c) = 0\), \(f'(c) \neq 0\) per qualche \(c \in [a,b]\). Allora esiste un \(\delta > 0\) tale per cui l’iterata (13) applicata ad \(f\) converge a \(c\) per ogni valore iniziale \(x_0 \in [c-\delta,c+\delta]\).

Ricordate queste caratteristiche iniziali, possiamo procedere ad implementare una versione MATLAB dell’algoritmo di Newton.

Esercizio 1

Si implementi in una funzione MATLAB l’algoritmo di Newton sfruttando l’iterata descritta in (13). Un template della funzione da implementare che si può adottare è quindi il seguente:

function [c,residuo] = newton(f,fp,x0,maxit,tol)
%%NEWTON Implementazione del metodo di Newton
% Input:  f function handle della funzione di cui si cerca lo zero
%         fp function handle della derivata prima della funzione
%         x0 approssimazione iniziale
%         maxit numero massimo di iterazioni consentite
%         tol tolleranza sul residuo
% Output: c vettore delle radici candidate prodotte dal metodo
%         residuo vettore dei residui prodotto dal metodo

end

È importante che la funzione implementata

• pre-allochi la memoria per i vettori c e residuo,

• riduca al minimo le chiamate ad \(f(\cdot)\).

Per testare l’algoritmo implementato si può usare

%% Script di test per il metodo di Newton
clear; clc;
f = @(x) x.^3 - 2*x - 5;
fp = @(x) 3*x.^2 -2;
maxit = 200;
tol = 1e-6;
ctrue = 2.09455148154232659;
x0 = 3;
[c,residuo] = newton(f,fp,x0,maxit,tol);

Da cui otteniamo

Iterata 1	c = 3.000000	residuo = 1.600000e+01
Iterata 2	c = 2.360000	residuo = 3.424256e+00
Iterata 3	c = 2.127197	residuo = 3.710998e-01
Iterata 4	c = 2.095136	residuo = 6.526626e-03
Iterata 5	c = 2.094552	residuo = 2.146143e-06
Iterata 6	c = 2.094551	residuo = 2.327027e-13
	Convergenza raggiunta in 6 iterazioni

Convergenza

Fig. 15 Paragone tra la convergenza del metodo di Newton e il metodo di bisezione per calcolare una radice di \(f(x) = x^3-2x-5\).

Possiamo confrontare il metodo di Newton con il metodo di bisezione implementato nella scorsa lezione, sfruttiamo lo stesso caso di test dell’Esercizio 1 e aggiungiamo allo script di test del metodo di Newton:

a = 1;
b = 3;
maxit = 200;
tol = 1e-6;
[c2,residuo2] = bisezione(f,a,b,maxit,tol);

n = 1:length(residuo);
n2 = 1:length(residuo2);
semilogy(n,abs(c-ctrue),'ro-',...
    n2,abs(c2-ctrue),'bx-','LineWidth',2);
legend({'Metodo di Newton','Metodo di Bisezione'},'FontSize',14);
xlabel('Iterazione')

per cui vediamo una rappresentazione in Fig. 15. Come ci aspettavamo dall’analisi teorica, il metodo di Newton è in questo caso di ordine \(2\). Possiamo investigare l’ordine di convergenza anche in maniera numerica.

Per farlo ricordiamo che una successione di approssimate \(\{x_n\}_n\) che converge ad \(x\) ha ordine di convergenza \(p \geq 1\) se

\[\lim_{n \rightarrow +\infty} \frac{|x_{n+1}-x|}{|x_n -x|^p} = c, \text{ con } c \in (0,1).\]

Possiamo sfruttare la definizione per ottenere una stima dell’ordine di convergenza mediante i rapporti tra gli errori a iterazioni successive. Questo può essere implementato in una funzione MATLAB come

function q = convergenza(xn, xtrue)
%%CONVERGENZA produce una stima dell'ordine di convergenza della
%%successione x_n ad xtrue.
  e = abs(xn - xtrue);
  q = zeros(length(e)-2,1);
  for n = 2:(length(e)-1)
      q(n-1) = log(e(n+1)/e(n))/log(e(n)/e(n-1));       
  end
end

E se lo applichiamo al vettore c e alla ctrue prodotta dal metodo di Newton otteniamo i valori

>> p = convergenza(c,ctrue)

p =

    1.7080
    1.9194
    1.9936
    1.9996

che ci conferma che l’ordine di convergenza si avvicina a \(2\).

Approssimare la derivata prima

Non sempre possediamo o possiamo calcolare in forma chiusa la derivata della funzione \(f\). Può essere utile approssimarla direttamente a partire utilizzando solo la \(f\). Possiamo farlo in maniera numerica sfruttando la definizione stessa di derivata:

(14)\[f'(x_k) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \approx \frac{f(x+h)-f(x)}{h}\]

prendendo un \(h\) sufficientemente piccolo, una buona scelta è \(h = \sqrt{\varepsilon}\) per \(\varepsilon\) la precisione di macchina.

Esercizio 2

Si modifichi il codice dell’Esercizio 1 per utilizzare l’approssimazione della derivata in (14).

Radici multiple

L’ordine di convergenza del metodo di Newton è ridotto quando la radice che \(c\) di \(f\) che cerchiamo ha molteplicità più elevata.

Suggerimento

Ricordiamo che se \(c\) è una radice di \(f\) la sua molteplicità è il più piccolo \(q\) per cui \(f^{(q)}(c) \neq 0\).

Ad esempio \(f(x) = (x-2)^2\), \(f(2) = 0\), \(f'(x) = 2(x-2)\), \(f'(2) = 0\), ma \(f''(x) = 2\) per cui \(f''(2) \neq 0\) e dunque la molteplicità è \(q=2\).

Possiamo modificare il metodo di Newton per recuperare l’ordine quadratico di convergenza se sappiamo la molteplicità \(q\) della radice che stiamo cercando. Si tratta di modificare l’iterazione come:

(15)\[x_{k+1} = x_k - q \frac{f(x_k)}{f'(x_k)}, \quad x_0 \text{ assegnato }, k \geq 1.\]

Esercizio 3

Si modifichi la funzione dell”Esercizio 1 con una che implementi l’iterazione (15). Cioè con una funzione che abbiamo tra gli input anche l’ordine \(q\) della radice.

Un prototipo della funzione è quindi

function [c,residuo] = mnewton(f,fp,x0,q,maxit,tol)
%%NEWTON Implementazione del metodo di Newton
% Input:  f function handle della funzione di cui si cerca lo zero
%         fp function handle della derivata prima della funzione
%         x0 approssimazione iniziale
%         q ordine della radice da calcolare
%         maxit numero massimo di iterazioni consentite
%         tol tolleranza sul residuo
% Output: c radici candidate prodotte dal metodo
%         residuo vettore dei residui prodotto dal metodo

end

Dopo averlo implementato possiamo testarlo con il seguente script

%% Script di test per il metodo di Newton modificato

clear; clc;

f = @(x) x.^3 + 2*x.^2 -7*x + 4;
fp = @(x) 3*x.^2 +4*x -7;
maxit = 200;
tol = 1e-6;

ctrue = 1;

x0 = 2;
[c,residuo] = newton(f,fp,x0,maxit,tol);

x0 = 2;
q = 2;
[cm,residuom] = mnewton(f,fp,x0,q,maxit,tol);

Per vedere la differenza nell’ordine di convergenza possiamo usare la funzione convergenza che abbiamo discusso nella sezione Convergenza e rappresentare di nuovo in maniera grafica il residuo.

q = convergenza(c,ctrue);
qm = convergenza(cm,ctrue);

figure(1)
subplot(1,2,1)
semilogy(1:length(residuo),residuo,'o-',...
    1:length(residuom),residuom,'x-','LineWidth',2);
xlabel('Iterazione')
ylabel('Errore Assoluto')
legend({'Newton','Newton Modificato'},'FontSize',16,...
    'Location','southeast');
subplot(1,2,2)
semilogy(3:length(residuo),q,'o-',...
    3:length(residuom),qm,'x-',...
    1:14,ones(14,1),'k--',...
    1:14,2*ones(14,1),'k--','LineWidth',2);
xlabel('Iterazione')
ylabel('Ordine di Convergenza Stimato')
legend({'Newton','Newton Modificato'},'FontSize',16,...
    'Location','southeast');
axis([1 14 0.8 2.2])

Quello che osserviamo dalla Fig. 16 è esattamente quanto previsto dalla teoria. La versione non modificata di Newton ha convergenza lineare, mentre la versione modificata ha un chiaro comportamento quadratico.

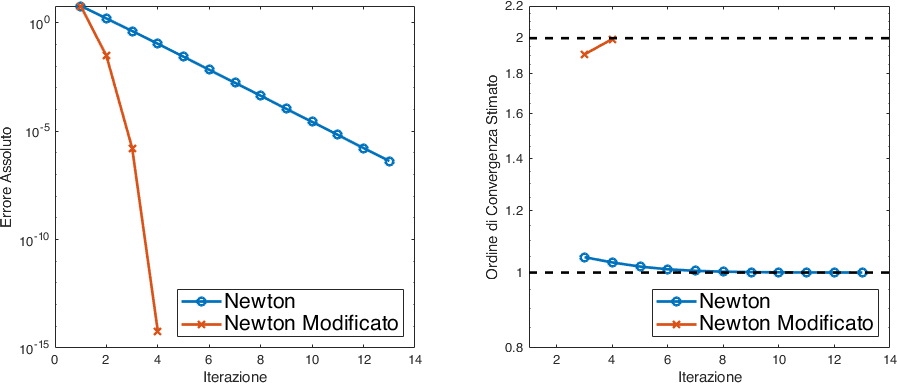
Fig. 16 Convergenza del metodo di Newton per radici multiple, confronto tra il caso standard e quello modificato.

Esempi di applicazioni

Consideriamo alcune applicazioni ingegneristiche del problema di trovare lo zero di una funzione [Kiu15].

Entalpia

L’energia libera di Gibbs (anche chiamata entalpia libera) è una funzione di stato termodinamica utilizzata per rappresentare l’energia libera nelle trasformazioni a pressione e temperatura costante. In termochimica è usata per determinare la spontaneità di una reazione.

Esercizio 4: Energia libera di Gibbs

L’energia libera di Gibbs di una mole di idrogeno alla temperatura \(T\) è

\[ G = - R T \ln[ (T/T_0)^{5/2}]\,J,\]

dove \(R = 8.31441\,J/K\) è la costante dei gas e la temperatura iniziale è \(T_0 = 4.44418\,K\). Si determini la temperatura a cui \(G = -10^{5}\,J\).

Sistema molle–ammortizzatore

Fig. 17 Un modello accoppiato molla-ammortizzatore.

Esercizio 5: Sistema molle–ammortizzatore

Consideriamo il sistema accoppiato di molle e ammortizzatori in Fig. 17. I due blocchi di massa \(m\) sono connessi tra di loro da due molle e da un ammortizzatore. Il coefficiente elastico di ognuna delle due molle è dato da \(k\), mentre \(c\) è il coefficiente che regola l’attenuazione causata dall’ammortizzatore. Quando il sistema è messo in posizione e rilasciato, la posizione di ogni blocco durante il moto ha la forma

\[x_k(t) = A_k e^{\omega_r t} \cos(\omega_i t + \phi_k), \qquad k=1,2,\]

dove \(A_k\) e \(\phi_k\) sono costanti, e \(\omega = \omega_r \pm i \omega_i\) sono le radici dell’equazione

\[\omega^4 + 2 \frac{c}{m} \omega^3 + 3 \frac{k}{m}\omega^2 + \frac{ c k}{m^2} \omega + \left(\frac{k}{m}\right)^2 = 0.\]

Si determinino le possibili combinazioni di \(w_r\) e \(w_i\) se \(c/m = 12\,s^{-1}\), e \(k/m = 1500 s^{-2}\).

Esercizio 6

Si re-implementino/modifichino gli esercizi del laboratorio3 cambiando dal metodo di Bisezione al metodo di Newton.

Bibliografia

Kiu15

Jaan Kiusalaas. Numerical Methods in Engineering with MATLAB®. Cambridge University Press, 3 edition, 2015. doi:10.1017/CBO9781316341599.