Laboratorio 11 : Metodi per la Soluzione di ODE#

In questo laboratorio ci vogliamo occupare di alcuni metodi per la soluzione di una equazione differenziale del primo ordine, la cui forma generale è

\[y' = f(x,y)\]

dove \(y' = {\rm d}y/{\rm d}x\) e \(f(x,y)\) è una funzione data. Come avete visto nei corsi di Analisi, la soluzione di questo tipo di equazioni contiene una costante arbitraria (detta costante di integrazione). Per trovare questa costante, e dunque determinare completamente una soluzione, dobbiamo sapere un punto sulla curva della soluzione:

\[y(a) = \alpha.\]

In modo più formale, un’equazione differenziale ordinaria di ordine \(p\), in forma normale, è un’equazione del tipo

\[y^{(p)}=f(x,y,y',y'',\ldots,y^{(p-1)}),\]

che lega una funzione \(y=y(x)\) e le sue derivate fino all’ordine \(p\).

Soluzione dell’equazione è una funzione \(y(x)\), continua e derivabile fino all’ordine \(p\) in un intervallo opportuno, che soddisfa l’equazione.

In generale, un’equazione differenziale ha infinite soluzioni. Solitamente si impongono delle condizioni aggiuntive e si determinano le soluzioni che soddisfano le condizioni assegnate.

Problema ai valori iniziali#

Nel problema ai valori iniziali, detto anche di Cauchy, all’equazione

\[y^{(p)}=f(x,y,y',y'',\ldots,y^{(p-1)}),\]

si assegnano \(p\) condizioni iniziali

\[ y(x_0)=\eta_0,\quad y'(x_0)=\eta_1,\quad\ldots\quad,y^{(p-1)}(x_0)=\eta_{p-1}.\]

Sotto opportune condizioni, si dimostrano l’esistenza e l’unicità della soluzione. In particolare, nel caso \(p=1\)

\[\begin{split} \left\{\begin{array}{l} y'=f(x,y)\quad\\y(x_0)=\eta \end{array} \right.\end{split}\]

valgono risultati di esistenza e unicità della soluzione nell’ipotesi che \(f(x,y)\) sia continua rispetto a \(x\) e uniformemente lipschitziana rispetto a \(y\).

Più in generale, possiamo guardare ad un sistema \(p\) equazioni differenziali del primo ordine

\[\begin{split} \left\{\begin{array}{l} y_1'=f_1(x,y_1,\ldots,y_p)\\ y_2'=f_2(x,y_1,\ldots,y_p)\\ \ldots\\ y_p'=f_n(x,y_1,\ldots,y_p)\\ \end{array}\right.\end{split}\]

dove \(f_1,\ldots,f_p\) sono \(p\) funzioni di \(p+1\) variabili e \(y_1(x), y_2(x),\ldots,y_p(x)\) sono le \(p\) incognite.

In forma compatta:

\[{\bf y}'={\bf f}(x,{\bf y}),\]

dove \({\bf y}\), \({\bf y}'\) e \({\bf f}\) sono vettori di funzioni.

Se a questo sistema associamo le condizioni iniziali

\[{\bf y}(x_0)=(\eta_0,\eta_1,\ldots,\eta_{p-1})^T,\]

otteniamo il corrispondente problema ai valori iniziali, che, sotto ipotesi simili a quelle già viste, ammette una e una sola soluzione.

Equazione differenziale \(\leadsto\) sistema di ordine 1

Data un’equazione differenziale di ordine \(p\)

\[y^{(p)}=f(x,y,y',y'',\ldots,y^{(p-1)}),\]

poniamo

\[y_1(x)=y(x),\quad y_2(x)=y'(x),\quad\ldots\quad y_p(x)=y^{(p-1)}(x).\]

Allora l’equazione si trasforma in un sistema di equazioni del primo ordine

\[\begin{split} \left\{\begin{array}{l} y_1'=y_2\\ y_2'=y_3\\ \ldots\\ y_{p-1}'=y_p\\ y_p'=f(x,y_1,y_2,\ldots,y_p) \end{array}\right.\end{split}\]

Metodi numerici#

Determinare la soluzione di un’equazione differenziale per via analitica è generalmente difficile e spesso impossibile. Per esempio, l’equazione

\[y'=x^2+y^2,\]

nonostante l’aspetto apparentemente semplice, non è risolubile in termini di funzioni elementari. Dobbiamo quindi cercare una soluzione approssimata usando un metodo numerico.

La letteratura che tratta i metodi numerici per equazioni differenziali con condizioni iniziali è molto vasta. Come primi esempi abbiamo visto

  • il metodo di Eulero esplicito,

  • il metodi di Eulero implicito,

  • il metodo di Crank-Nicolson.

Il metodo di Eulero esplicito#

Consideriamo il problema di Cauchy

\[\begin{split} \left\{\begin{array}{l} y'=f(x,y)\\y(a)=\eta \end{array} \right.\end{split}\]

che vogliamo risolvere numericamente nell’intervallo \([a,b]\). Discretizziamo la variabile \(x\) fissando, nell’intervallo \([a,b]\), una griglia di nodi \(\{x_n\}_{n=0,\ldots,N}\) equidistanti di passo \(h>0\):

\[ x_0=a,\quad x_n=x_{n-1}+h,\quad x_N=b.\]

Il comportamento della soluzione \(y(x)\) tra \(x_{n}\) e \(x_{n+1}\) può essere stimato come

\[ y(x_{n+1})\sim y(x_{n})+hf(x_{n},y(x_{n})).\]

Per cui si approssima la funzione \(y(x)\) per mezzo dei suoi valori \(y_{n}\) nei nodi \(x_{n}\), calcolati tramite la formula

\[y_0=\eta,\quad y_{n+1}=y_{n}+hf(x_{n},y_{n}),\quad n=0,\ldots,N-1.\]

Abbiamo ora tutti gli strumenti necessari ad implementare il metodo di Eulero esplicito.

Esercizio

Si usi il seguente prototipo per implementare il metodo di Eulero esplicito per un’equazione differenziali del primo ordine.

function [y,x] = expliciteuler(f,y0,a,b,h)
%%EXPLICITEULER implementa il metodo di Eulero esplicito per la soluzione
% di un'equazione differenziale del primo ordine.
%   INPUT: f function handle della dinamica del sistema f(x,y)
%          y0 vettore delle condizioni iniziali
%          a,b estremi dell'intervallo di integrazione
%          h ampiezza del passo di integrazione
%   OUTPUT: y vettore che contiene le soluzioni calcolate nei
%           punti x(n),
%           x vettore dei nodi

end

  • Si minimizzi il numero di chiamate alla funzione \(f\).

Per testare il codice si può usare il seguente problema di test

\[\begin{split} \left\{\begin{array}{l} y'=-\frac{2y+x^2y^2}{x}\\ y(1)=1 \end{array}\right.\end{split}\]

per \(x\in [1,2]\). In questo caso la soluzione esatta è nota e vale

\[y=\frac{1}{x^2(\log x+1)}.\]
%% Il metodo di Eulero esplicito
f = @(x,y) - (2*y + (x^2)*(y^2))/(x);
ytrue = @(x) 1./(x.^2.*(log(x)+1));

a = 1;
b = 2;
h  = 1e-2;
y0 = 1;
[y,x] = expliciteuler(f,y0,a,b,h);

figure(1)
plot(x,y,'r--',x,ytrue(x),'b-','LineWidth',2);
xlabel('x');
legend({'Computed Solution','True Solution'},'FontSize',14);
figure(2)
semilogy(x,abs(y-ytrue(x)),'r-','LineWidth',2);
xlabel('x');
ylabel('Errore Assoluto');

Possiamo studiare la convergenza del metodo guardando all’errore rispetto alla soluzione esatta e sfruttando la function convergenza2 che abbiamo visto quando abbiamo discusso del metodo di Newton (Convergenza) per stimare numericamente l’ordine di convergenza:

function q = convergenza2(x)
%%CONVERGENZA produce una stima dell'ordine di convergenza della
%%successione x_n ad xtrue.
    q = zeros(length(x)-3,1);
    for n = 3:(length(x)-1)
        q(n-1) = real(log((x(n+1)-x(n))/(x(n)-x(n-1)))/log((x(n)-x(n-1))/(x(n-1)-x(n-2))));       
    end
end

Con questa osserviamo che:

%% Convergenza
k = 9;
h = fliplr(logspace(-6,-1,k));
err = zeros(k,1);
for i=1:k
    [y,x] = expliciteuler(f,y0,a,b,h(i));
    yt = ytrue(x);
    err(i) = norm(y - yt)/norm(yt);
end

figure(3)
loglog(h,err,'o-');
xlabel('h')
ylabel('Errore Assoluto');

q = convergenza2(err);
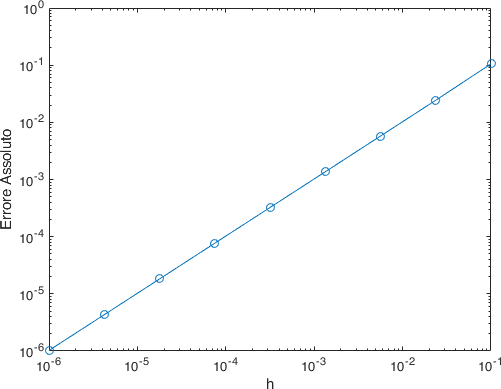
_images/forward_euler_error.png

Fig. 18 Errore del metodo di Eulero in avanti.#

ed il valore di \(q = [0.9784, 0.9972, 1.0000, 1.0001, 1.0000, 1.0000]\) ed il previsto ordine di convergenza per questo metodo.

Infatti, se supponiamo che \(f(x,y)\) abbia derivate continue rispetto a \(x\) e \(y\). In questo caso si ha \(y(x)\in\mathcal{C}^2([a,b])\). Possiamo quindi applicare la formula di Taylor (con resto in forma di Lagrange):

\[y(x_{n+1})-y(x_{n})=hy'(x_{n})+\frac{h^2}{2}y''(\xi),\quad \xi\in (x_{n},x_{n+1})\]

da cui si deduce

\[|\tau_{n+1}|=\frac{h}{2}|y''(\xi)|.\]

Quindi in ogni intervallo \([x_{n},x_{n+1}]\) l’errore locale è approssimativamente lineare in \(h\). Poiché \(|y''(\xi)|\) è limitato in \([a,b]\), si ha che \(\tau_{n+1}\) tende a zero con \(h\) e si scrive \(\tau_{n+1}=\mathcal{O}(h)\).

Posto \(\tau=\max_{n=1,\ldots,N}|\tau_n|\), esiste una costante \(M\neq 0\) per cui \(\tau\leq Mh\), e quindi

\[ \lim_{h\rightarrow 0}\tau=0,\qquad \tau=\mathcal{O}(h).\]

Si dice allora che il metodo di Eulero è consistente di ordine 1.

Si può dimostrare che, sotto le stesse ipotesi su \(f\), anche l’errore globale tende a zero con \(h\rightarrow 0\). Concludiamo quindi che il metodo di Eulero è convergente.

Il metodo di Eulero implicito#

Nel metodo di Eulero all’indietro la funzione \(y(x)\) viene approssimata tramite la formula

\[y_0=\eta,\quad y_{n+1}=y_{n}+hf(x_{n+1},y_{n+1}),\quad n=0,\ldots,N-1.\]

Esercizio

Si implementi il metodo di Eulero implicito.

function [y,x] = impliciteuler(f,y0,a,b,h)
%%IMPLICITEULER implementa il metodo di Eulero implicito per la soluzione
% di un'equazione differenziale del primo ordine.
%   INPUT: f function handle della dinamica del sistema f(x,y)
%          y0 vettore delle condizioni iniziali
%          a,b estremi dell'intervallo di integrazione
%          h ampiezza del passo di integrazione
%   OUTPUT: y vettore che contiene le soluzioni calcolate nei
%           punti x(n),
%           x vettore dei nodi

end

  • Si usi il comando fsolve per risolvere il sistema (possibilmente) non lineare. Si usi l’approssimazione al passo precedente come dato iniziale per il metodo. Per sopprimere le stampe di controllo di fsolve si possono usare le opzioni generate con optimoptions('fsolve','Display','none').

Si implementi una function impliciteulernewton con gli stessi input ed output della funzione precedente ma che utilizza il metodo di Newton per la risoluzione del sistema non lineare risultante dall’approssimazione con Eulero implicito. Si usi l’approssimazione al passo precedente come dato iniziale per il metodo di Newton.

Per verificare l’implementazione possiamo usare lo stesso problema test

%% Il metodo di Eulero implicito
f = @(x,y) - (2*y + (x^2)*(y^2))/(x);
ytrue = @(x) 1./(x.^2.*(log(x)+1));

a = 1;
b = 2;
h  = 1e-2;
y0 = 1;
[y,x] = impliciteuler(f,y0,a,b,h);

figure(1)
plot(x,y,'r--',x,ytrue(x),'b-','LineWidth',2);
xlabel('x');
legend({'Computed Solution','True Solution'},'FontSize',14);
figure(2)
semilogy(x,abs(y-ytrue(x)),'r-','LineWidth',2);
xlabel('x');
ylabel('Errore Assoluto');

Esercizi#

Esercizio

Un veicolo spaziale è lanciato ad una altitudine di \(H = 772 \text{ km}\) sul livello del mare con velocità iniziale \(v_0 = 6700\,\text{m/s}\) nella direzione illustrata in Fig. 19. Le equazioni differenziali che descrivono il moto dell’oggetto in coordinate polari sono

\[\ddot{r} = r \dot{\theta}^2 - \frac{G M_e}{r^2}, \quad \ddot{\theta} = - 2 \frac{\dot{r}\dot{\theta}}{r}.\]

Rispetto alle costanti

  • \(G = 6.672 \times 10^{-11}\) \(\text{m}^3\text{kg}^{-1}\text{s}^{-2}\) per la costante di gravitazione universale,

  • \(M_e = 5.9742 \times 10^{24} \text{ kg}\), per la massa della terra,

  • \(R_e = 6378.14 \text{ km}\) per il raggio della terra a livello del mare,

Si ottengano le equazioni differenziali del primo ordine per questo sistema e si integri numericamente fino a che il veicolo non tocca terra. Si determini il valore di \(\theta\) del sito di impatto.

Suggerimento

Si può usare il seguente prototipo per implementare la dinamica. In questa implementazione assumiamo di aver ordinato le variabili \(\mathbf{y}\) del sistema riscritto al primo ordine come \(\mathbf{y} = [y_1,y_2,y_3,y_4]^T = [r,\dot{r},\theta,\dot{\theta}]^T\).

function ydot = veicolo(x,y)
%VEICOLO Dinamica per il veicolo in coordinate polari.
%   INPUT:  x variabile muta
%           y vettore delle variabili y = [r rdot theta thetadot]
%   OUTPUT: dinamica del sistema

end

Esercizio

Un paracadutista di massa \(m\) in caduta libera verticale subisce una resistenza aerodinamica \(F_D = c_D \dot{y}^2\), dove \(y\) è misurata verso il basso dall’inizio della caduta. L’equazione differenziale che descrive la caduta è

\[\ddot{y} = g - \frac{c_D}{m} \dot{y}^2.\]

Si determnini il tempo di una caduta di \(500 \text{ m}\) utilizzando \(g = 9.80665 \text{ m/}\text{s}^2\), \(c_D = 0.2028 \text{ kg/m}\) e \(m = 80 \,\text{kg}\).