Laboratorio 4 e 5: Metodi di Interpolazione

In molti problemi si ha a che fare con una funzione \(f:\mathbb{R}\rightarrow\mathbb{R}\) di forma non elementare, o addirittura sconosciuta, di cui si possiede solo una tabulazione in un insieme finito di punti, per esempio derivanti da misurazioni sperimentali. In questi casi la stima di un valore di \(f\), in un punto diverso da quelli in cui è data, può essere fatta utilizzando i dati disponibili. Questa operazione si effettua sostituendo a \(f\) una funzione che sia facilmente calcolabile come, per esempio, un polinomio.

Supponiamo siano dati \(n+1\) punti reali \(x_0,\ldots, x_n\in [a,b]\subset\mathbb{R}\), due a due distinti, in corrispondenza dei quali siano noti gli \(n+1\) valori reali \(f(x_0), \ldots, f(x_n)\). L’interpolazione polinomiale consiste nel determinare un polinomio \(P_n\) di grado al più \(n\) tale che

(4)\[P_n(x_i)=f(x_i),\quad \forall i=0,1,\ldots,n.\]

Srivendo il polinomio \(P_n\) nella base dei monomi \(\{1,x,x^2,\ldots\}\) si ha

\[P_n(x)=a_n x^n+a_{n-1} x^{n-1}+\ldots+a_1 x+a_0,\]

i cui coefficienti \(\{a_i\}_{i=0}^n\) si possono ricavare risolvendo il sistema lineare di \(n+1\) equazioni ottenuto imponendo che il polinomio verifichi le condizioni di interpolazione (4), ovvero chiedendo che \(P_n(x_i) = y_i\) per \(i=1,\ldots,n+1\), si ottiene:

\[ P_n(x_i) = \sum_{j=1}^{n+1} x_i^{(j-1)} a_j = f(x_i) = y_i\quad \Longrightarrow\quad V a = y \]

Dove la matrice \(V\)

\[ V_{ij} = x_i^{(j-1)}, \qquad i,j = 1,\ldots,n+1 \]

è nota come matrice di Vandermonde.

Dati i punti di interpolazione x e i valori y, i coefficienti del polinomio che interpola y nei punti x sono quindi dati da

\[ a = A^{-1} y, \]

che in matlab può essere calcolato con

a = A\y

Esercizio 1

Si implementi una function che, dati i punti di interpolazione come vettore riga x di dimensione \(n+1\), costruisce la matrice di Vandermonde \(V\) tale che size(V) = (n+1,n+1).

Si calcoli il suo numero di condizionamento sui punti di interpolazione x = linspace(0,1,n+1) al variare di n. Quando il numero di condizionamento supera 1/eps?

Si usi il seguente prototipo

function V = Vandermonde(x)
%%VANDERMONDE costruisce la matrice di Vandermonde V
%    INPUT:
%          x vettore riga degli n+1 nodi di interpolazione
%   OUTPUT:
%          V matrice di Vandermonde
end

Poiché la matrice di Vandermonde risulta una matrice malcondizionata non conviene risolvere il sistema lineare per determinare il polinomio di interpolazione. Si preferisce cambiare la base in cui rappresentiamo i polinomi, in modo che la matrice di interpolazione sia l’identità.

Per fare questo, costruiamo il polinomio di interpolazione di grado al più \(n\) della forma

\[P_n(x) = \sum_{j=0}^n f(x_j)\ell_j(x),\qquad \ell_j(x)=\prod_{i\neq j}\dfrac{x-x_i}{x_j-x_i}.\]

Esercizio 2

Si implementi una function che costruisce le funzioni polinomiali \(\ell_j\) dato il vettore x di \(n+1\) nodi di interpolazione e restituisce il suo valore nei punti specificati nel vettore z. Si segua il seguente prototipo

function L = LagrangePoly(x, z, j)
%%LAGRANGEPOLY costruisce il j-esimo polinomio di Lagrange dati i nodi
% di interpolazione x e lo valuta nei vettore z
%    INPUT:
%          x vettore riga degli n+1 nodi di interpolazione
%          z vettore riga dei punti di valutazione del polinomio
%          j indice the polinomio di Lagrange
%   OUTPUT:
%          L j-esimo polinomio di Lagrange valutato in z
end

• Si inserisca un controllo sul valore di \(j\) ammesso.

Si usi la function LagrangePoly per costruire il polinomio di interpolazione di Lagrange \(P_3\) dai punti di interpolazione di Tabella 1

\[\begin{split}\begin{aligned} &\text{Tabella 1}\\ &\begin{array}{c|ccccc} x_i & -5 & -4 & 0 & 5 \\ \hline y_i & -1 & -1 & -16 & 0\\ \end{array} \end{aligned}\end{split}\]

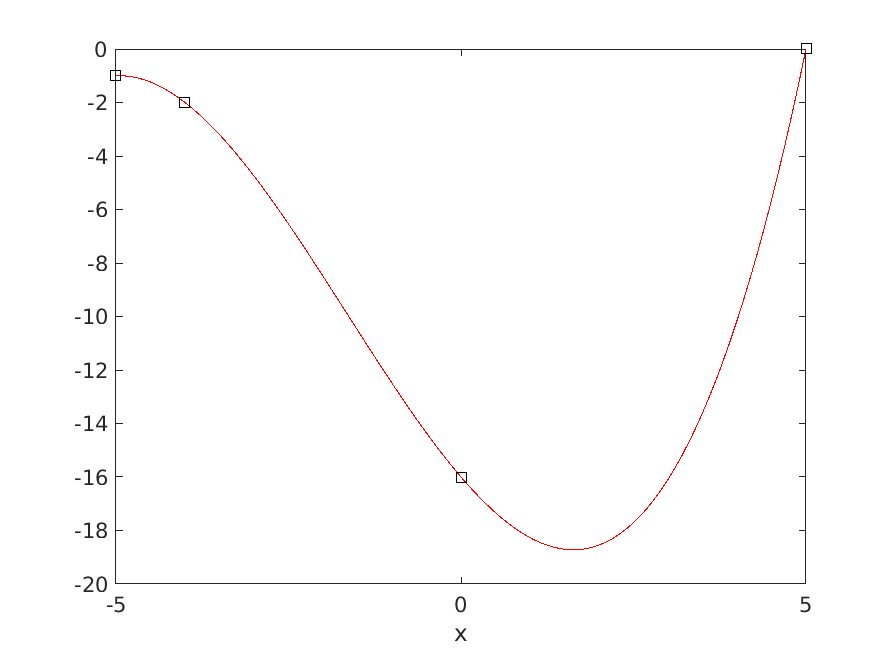
Si implementi uno script di MATLAB che produce il grafico del polinomio di interpolazione \(P_3\) nell’intervallo \([-5,5]\) con \(m=100\) punti equidistanti. Si aggiungano alla stessa figura i punti di interpolazione.

Il grafico risultante è mostrato qui sotto.

Per trovare i coefficienti del polinomio interpolante nella base dei monomi esistono le seguenti routine di MATLAB:

• a = polyfit(xData,yData,m) restituisce il vettore a di coefficienti del polinomio di grado \(m\) che approssima i dati (xData,yData).

• y = polyval(a,x) valuta nel punto x il polinomio definito dai coefficienti a.

Esercizio 3

Si consideri la funzione di Runge

(5)\[f(x) = \dfrac{1}{1+x^2},\quad x\in[a,b].\]

Vogliamo studiare l’influenza della scelta dei nodi di interpolazione sulla qualità dell’interpolante polinomiale di grado \(n\) per diversi valori di \(n\).

Si implementi uno script di MATLAB in cui:

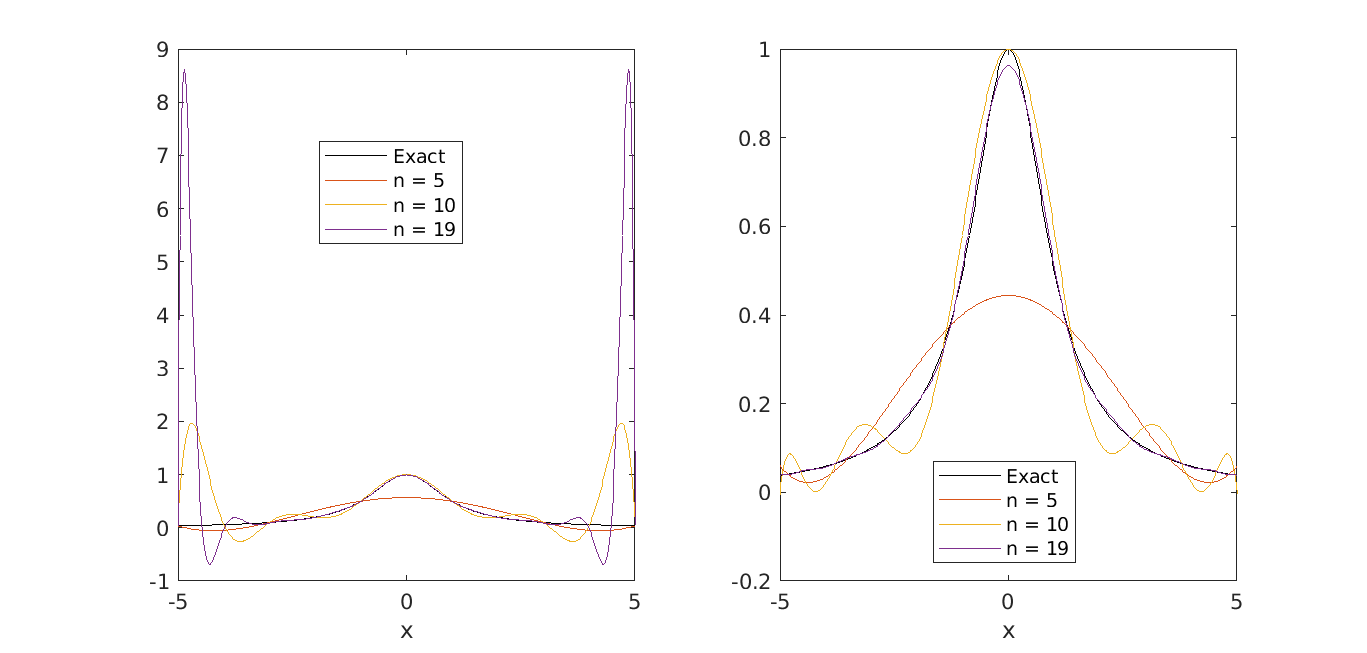
• Si calcolino i polinomi \(\{P_n\}_n\) di Lagrange di grado \(n=5,10,19\) che interpolano la funzione data in (5) usando \(n+1\) nodi equispaziati nell’intervallo \([−5, 5]\). Si riporti il grafico di ciascun polinomio interpolante su \(m=500\) punti nell’intervallo considerato, insieme con quello della funzione data;

• Si calcoli per ciascun valore di \(n\) l’errore commesso ossia \(E_n = \max_{-5\leq x \leq 5} |f(x) − P_n(x)|\) e si riportino gli errori ottenuti in un grafico in scala semilogaritmica;

• Si utilizzi l’implementazione dell’interpolazione di Lagrange derivata nell’Esercizio 2.

Un suggerimento

Si può seguire il seguente prototipo

a = -5;
b = 5;
m = 500;
z = ... % punti di valutazione
f = ... % funzione di Runge definita come handle function
d = [5,10,19];
% Allocazione dei polinomi interpolanti e del vettore degli errori
P = ...
err = ...
for k = 1:length(d)
    ...
    
    x = ...  % Nodi di interpolazione
    ...

    % Calcolo del polinomio di Lagrange
    ...
    
    % Calcolo dell'errore
    ...
end
% Plot della funzione e dei polinomi interpolanti
...
legend('Exact','n = 5','n = 10','n = 19','Location','best');
% Plot dell'errore
...

Il fenomeno che si osserva nell’Esercizio 3 è la mancata convergenza della successione \(\{P_n\}_n\) dei polinomi di interpolazione alla funzione di Runge (5). Tale fenomeno, detto anche fenomeno di Runge, può essere evitato utilizzando opportune distribuzioni di nodi.

Nell’intervallo \([a,b]\subset\mathbb{R}\) si considerino i nodi \(\{x_i\}_{i=0}^{n}\) dati da

(6)\[x_i = \dfrac{a+b}{2} + \dfrac{b-a}{2}\widehat{x}_i\quad\mbox{con}\;\widehat{x}_i = -\cos\left(\dfrac{\pi i}{n}\right),\quad i=0,\ldots,n.\]

I punti \(\widehat{x}_i\in[−1, 1]\) sono detti nodi di Chebyshev.

Esercizio 4

Si ripeta l’Esercizio 3 utilizzando come nodi di interpolazione i nodi di Chebyshev dati dalla (6).

I grafici dei polinomi interpolanti ottenuti con nodi di interpolazione equidistanti (grafico di sinistra) e con nodi di Chebyshev (grafico di destra) sono riportati qui sotto.

Esercizio 5

Si costruisca una funzione che valuta la funzione di Lebesgue \(\Lambda(x)\) definita come

\[ \Lambda(x) := \sum_{i=1}^{n+1} |\ell_i(x)|. \]

Si usi il seguente prototipo, insieme alla funzione costruita nell’esercizio 2:

function L = Lebesgue(x, z)
%%LEBESGUE costruisce la lebesgue function dati i nodi
% di interpolazione x e lo valuta nei vettore z
%    INPUT:
%          x vettore riga degli n+1 nodi di interpolazione
%          z vettore riga dei punti di valutazione della Lebesgue function
%   OUTPUT:
%          L la funzione di Lebesgue in z
end

Si plotti la funzione di Lebesgue per \(n=5,10,15\) su m=500 punti nell’intervallo -1,1, utilizzando i punti di interpolazione equispaziati (caso 1), e i punti di interpolazione di Chebyshev (caso 2).

Si costruisca un grafico in scala logaritmica che mostra il variare di \(\max_{x} |\Lambda(x)|\) nell’intervallo considerato al variare di \(n\) nei due casi.

\[\]