Laboratorio 3 : L’Aritmetica di Precisione Finita

Ricordiamo che l’artimetica floating point (floating-point arithmetic) è l’artimetica che fornisce una rappresentazione approssimata dei numeri reali per supportare un compromesso tra l’intervallo dei numeri rappresentati e la precisione ottenibile nei calcoli. Per questo motivo, il calcolo in virgola mobile viene spesso utilizzato in sistemi in cui si deve coniugare la rappresentazione di numeri in un ampio range richiedendo tuttavia tempi di elaborazione rapidi.

Un numero in virgola mobile è rappresentato approssimativamente da un numero fisso di cifre significative (il significando) e scalato usando un esponente in una qualche base fissata. Tale base è normalmente due, dieci o sedici. Un numero che può essere rappresentato esattamente è della forma seguente:

(1)\[ \text{significando} \times \text{base}^{\text{esponente}}.\]

Di tutte le possibili costruzioni di questo tipo, noi adoperiamo quella codificata nello standard IEEE-754 [IEEE75419], in cui (la maggior parte dei) i numeri floating point sono normalizzati, cioè possono essere espressi come

(2)\[x = \pm (1+f) 2^e, \qquad 0 \leq f < 1, \qquad -1022 \leq e \leq 1023,\]

dove \(f\) è detta la mantissa, e deve essere rappresentabile con al più 52 bits, cioè \(2^{52}f\) è un intero nell’intervallo \(0 \leq 2^{52} f < 2^{53}\), abbiamo fissato la base a \(2\) e chiamato l’esponente \(e\).

Il testo di riferimento per questi argomenti è [Hig02].

MATLAB implementa diversi formati di numeri floating point e interi; si veda la Tabella 8 per i diversi tipi di interi disponibili e le relative funzioni di conversione. In generale assumeremo di star lavorando con l’aritmetica in precisione doppia (double): cioè di usare una rappresentazione con 64 bits. Specificamente, il bit 63 assume valore \(0\) o \(1\) per indicare il segno (\(0\) se positivo, \(1\) se negativo). I bits da 62 a 52 contengono l’esponente \(e\), mentre i bits da 51 a 0 contengo la mantissa \(f\) come illustrato in (2).

Avvertimento

In alcuni casi MATLAB deciderà autonomamente se la variabile che stiamo usando è un intero e applicherà in tal caso l’aritmetica relativa. Alcune funzioni utili a verificare che tipo di aritmetica stiamo usando sono le funzioni isfloat e isinteger che restituiscono vero (\(1\)) se l’argomento è rispettivamente un floating point (single o double), oppure una delle tipologie di intero, falso (\(0\)) altrimenti.

Classi Numeriche

Tabella 8 Classi di numeri interi

Classe	Range	Conversione
Signed 8-bit integer	\(-2^7\) a \(2^7-1\)	int8
Signed 16-bit integer	\(-2^{15}\) a \(2^{15}-1\)	int16
Signed 32-bit integer	\(-2^{31}\) a \(2^{31}-1\)	int32
Signed 64-bit integer	\(-2^{63}\) a \(2^{63}-1\)	int64
Unsigned 8-bit integer	\(0\) a \(2^{8}-1\)	uint8
Unsigned 16-bit integer	\(0\) a \(2^{16}-1\)	uint16
Unsigned 32-bit integer	\(0\) a \(2^{32}-1\)	uint32
Unsigned 64-bit integer	\(0\) a \(2^{64}-1\)	uint64

Rappresentazione dei numeri di macchina

In generale non tutti i numeri potranno essere espressi nella forma (1), possiamo scegliere ad esempio il numero \(4/3\) che non può essere scritto esattamente nella forma \(s \times 2^k\). Se proviamo ad eseguire l’operazione

e = 1 - 3*(4/3 - 1)

da cui ci aspetteremo di ottenere uno \(0\), otteniamo invece

e =
   2.2204e-16

che è un errore della grandezza della precisione di macchina per l’aritmetica in virgola mobile adoperata da MATLAB.

In maniera analoga, possiamo considerare un altro numero che non è esattamente rappresentato in macchina \(0.1\). Se lo sommiamo \(10\) volte in aritmetica esatta ci aspettiamo di ottenere \(1\):

a = 0.0;
for i = 1:10
  a = a + 0.1;
end

Tuttavia se proviamo a fare la verifica leggiamo

a == 1
ans =

  logical

   0

Ed infatti,

abs(a-1)

ans =

   1.1102e-16

che è di nuovo dell’ordine della precisione di macchina.

Suggerimento

Quando impostiamo dei confronti di «uguaglianza» tra numeri floating point la procedura corretta è sempre quella di controllare la differenza in valore assoluto tra il valore calcolato ed il risultato aspettato in termine della precisione di macchina in uso:

abs(1-a) < eps

ans =

 logical

  1

che ci restituisce il valore aspettato, dove eps è spesso chiamato floating-point zero.

All’altro estremo del range dinamico dei numeri rappresentati osserviamo anche il problema del «diradarsi» dei numeri di macchina, infatti sfruttando la definizione di numero normalizzato osserviamo facilmente che:

(2^53 + 1) - 2^53

ans =
     0

Possiamo farci dire da MATLAB quali sono il più piccolo ed il più grande numero reale rappresentato richiamando le variabili realmin e realmax:

>> realmin

ans =

  2.2251e-308

>> realmax

ans =

  1.7977e+308

Qualunque operazione generi un numero maggiore di realmax provocherà un errore di overflow, qualunque operazione generi un numero minore di realmin genererà un errore di underflow. In MATLAB questo è rappresento dai valori +Inf e -Inf:

realmax + .0001e+308
ans =
   Inf

-realmax - .0001e+308
ans =
  -Inf

Avvertimento

Alcune macchine permettono il trattamento di alcuni casi eccezionali di numeri floating point, cioè l’esistenza di numeri denormalizzati (o subnormali). Questi si trovano nell’intevallo [eps*realmin,realmin].

L’ultimo caso che vogliamo discutere riguarda l’uso delle funzioni trigonometriche. Dalla goniometria di base sappiamo che \(\sin(k \pi) = 0\) per ogni \(k\) dispari. Tuttavia è immediato osservare che

sin(3*pi)

ans =

     3.673940397442059e-16

Poiché di \(\pi\) abbiamo solo un”approssimazione, l’algoritmo che calcola la funzione \(\sin(x)\) propaga l’errore commesso nell’argomento anche sulla valutazione restituendoci un errore finale dell’ordine della precisione di macchina.

D’altra parte, se usiamo la variante della funzione che lavora con i gradi, osserviamo che

sind(3*180)

ans =

     0

questa volta l’input della funzione è un intero, per cui non commettiamo errore di troncamento e otteniamo alla fine il valore esatto.

Associatività delle operazioni

Mentre l’operazione di somma e di prodotto sono garantite essere commutative nello standard IEEE, l’operazione di soma tra floating point è sicuramente non associativa. Si consideri infatti l’esempio:

b = 1e-16 + 1 - 1e-16;
c = 1e-16 - 1e-16 + 1;
b == c
ans =

  logical

   0

Si osserva che se andiamo a valutare la differenza tra le due procedure

>> abs(b-c)

ans =

   1.1102e-16

che è di nuovo dell’ordine della precisione di macchina.

Suggerimento

Quando si calcola la somma di più termini di ordine diverso è opportuno valutare l’accumulazione ed agire di conseguenza.

Precisione di stampa

È utile in alcuni casi aumentare la precisione delle stampe in uscita di MATLAB, possiamo farlo per mezzo del comando format, in particolare:

format long

farà in modo che l’output sia stampato con 15 cifre per una variabile di tipo double e con 7 cifre per una variabile di tipo single. Per tornare invece alla notazione di default si può usare il comando

format short

che userà invece 5 cifre indipendentemente per i due tipi di variabili. Altre opzioni si possono leggere facendo help format.

Pericolo

L’uso del comando format non altera la precisione in cui le operazioni sono compiute, ma solo il formato di stampa a schermo.

Per correggere il problema precedente si può implementare l”algoritmo delle somme compensate di Kahan, per cui uno pseudocodice è dato da:

function KahanSomma(input)
    somma = 0.0                  // variabile che conterrà la somma finale
    c = 0.0                      // Compensazione per i bits che altrimenti andrebbero persi.

    for i = 1 to length(input) do // L'array che ha in input le quantità da sommare va da input(1)
                                   // fino a input(length(input))
        y = input(i) - c           // Al primo passaggio c è zero
        t = somma + y              // Purtroppo, somma è "grande", y è piccolo, quindi alcuni bits
                                   // sono persi, ma non per sempre...
        c = (t - somma) - y        // (t - somma) cancella la parte di ordine alto di y; sottrarre y
                                   // recupera la parte "piccola" di y
        somma = t                  // In aritmetica di precisione infinita c dovrebbe essere
                                   // sempre zero
    // Alla prossima iterata la parte "persa" verrà aggiunta ad y in un nuovo
    // tentativo di recuperarla.
    end for

    return somma

Esercizio

Si implementi l’algoritmo KahanSomma in una funzione MATLAB e se ne verifichino le proprietà numeriche.

function [somma] = KahanSomma(input)
%%KAHANSOMMA algoritmo delle somme compensate di Kahan

end

Che possiamo testare sull’esempio precedente costruendo uno script con

clear; clc;

input = [ 1e-16 +1 -1e-16];

somma1 = input(1)+input(2)+input(3);
somma2 = sum(input);
somma3 = KahanSomma(input);

e confrontando la differenza in valore assoluto tra i tre valori somma1, somma2 e somma3. Cosa si osserva?

Per questo algoritmo è possibile dare una limitazione dell’errore commesso. Se chiamiamo

\[S_n = \sum_{i=1}^{n} \text{input}_i\]

la somma calcolata in precisione infinita, allora con un algoritmo otteniamo in genere \(S_n + E_n\) dove l’errore \(E_n\) può essere limitato per l’algoritmo delle somme compensate da

\[|E_n| \leq [2 \varepsilon + O(n\varepsilon^2)] \sum_{i=1}^{n} |\text{input}_i|,\]

dove \(\varepsilon\) è la precisione di macchina. Più in generale, siamo di solito interessati all’errore relativo, cioè alla quantità

\[\frac{|E_n|}{|S_n|} \leq [2 \varepsilon + O(n\varepsilon^2)] \frac{\sum_{i=1}^{n} |\text{input}_i|}{\left| \sum_{i=1}^{n} \text{input}_i| \right|},\]

Numero di condizionamento

Ricordiamo che il numero di condizionamento di un problema rappresenta essenzialmente la «sensitività» intrinseca del problema, indipendentemente dall’algoritmo utilizzato per risolverlo.

dove la quantità \(\kappa = \frac{\sum_{i=1}^{n} |\text{input}_i|}{\left| \sum_{i=1}^{n} \text{input}_i| \right|}\) rappresenta il numero di condizionamento dell’operazione di somma. Esistono algoritmi per la somma che esibiscono migliori limitazioni dell’errore [Kle06, Neu74] , per i nostri scopi illustrativi questa versione è sufficiente.

Errori di cancellazione/roundoff

Un altro caso in cui calcoli avventati possono avere effetti catastrofici è quello delle sottrazioni eseguite con operandi quasi uguali, è facile che l’annullamento si verifichi in modo imprevisto. Consideriamo l’esempio:

sqrt(1e-16 + 1) - 1

ans =
     0

in cui osserviamo una cancellazione causata da swamping, che è un fenomeno analogo a quello che abbiamo visto per l’associatività della somma. Stiamo osservando una perdita di precisione che rende l’aggiunta insignificante. È possibile introdurre delle correzioni algoritmiche in maniera analoga a quanto fatto per la somma anche per altre funzioni, per corregere l’esempio visto sopra possiamo usare la seguente riscrittura:

\[\sqrt{1e-16 + 1} - 1 = \exp( \log(\sqrt{1e-16 + 1}) ) - 1 = \exp( 0.5 \log(1e-16 + 1) ) - 1,\]

ed usare le funzioni expm1 e log1p di MATLAB che ci permettono di risolvere il problema di cancellazione:

expm1(0.5*log1p(1e-16))

in particolare

• expm1 calcola \(\exp(x)-1\) compensando per il roundoff in \(\exp(x)\),

• log1p calcola \(\log(1+x)\) evitando di calcolare \(1+x\) per valori «piccoli» di \(x\).

Roundoff polinomio

Consideriamo un altro esempio, produciamo uno script che valuti il seguente polinomio

(3)\[p(x) = x^7 - 7x^6 + 21x^5 -35x^4 +35x^3 - 21x^2 +7x -1,\]

nell’intervallo \([0.988,1.012]\) su di una griglia con scansione \(10^{-4}\). Come si vede dalla figura al margine questo produce il plot di una funzione che non sembra proprio essere un polinomio: non è liscia! Stiamo osservando di nuovo degli errori di roundoff dati dalla sottrazione di numeri dello stesso ordine (elevato), che infatti (come si legge dalla scala sull’asse delle \(y\)) hanno un ordine di \(10^{-14}\). Se guardiamo meglio al polinomio in (3) possiamo osservare che questo non è nient’altro che l’espansione di \(p(x) = (x-1)^7\), provate a fare un plot sullo stesso intervallo e confrontiamolo con il precedente

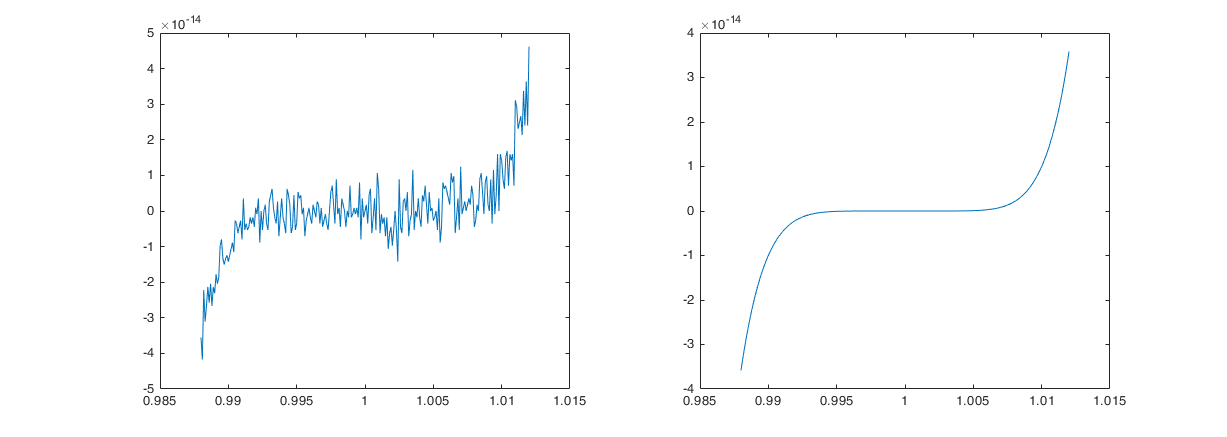
Fig. 3 Confronto del grafico del polinomio (3) calcolato nella forma (3) e a partire dalla forma \(p(x) = (x-1)^7\).

Precisione mista

La rivoluzione delle applicazioni di «apprendimento automatico» (machine learning) e dell’intelligenza artificiale (AI) ha suscitato negli ultimi anni un interesse per lo sviluppo di aritmetica a mezza precisione (formato in virgola mobile a 16 bit) che potesse rispondere al problema della necessità di avere alte prestazioni nelle fasi di addestramento delle reti neurali. L’idea nasce dall’osservazione (per lo più empirica) che dice che la maggior parte di queste applicazioni non richiede necessariamente l’accuratezza della precisione singola (single) o doppia (double). La mezza precisione (half) ha quindi un’aritmetica più veloce e produce una riduzione della memoria e del traffico di un fattore \(2\times\) contro il formato precisione in singola cifra e di un fattore \(4\times\) contro la doppia precisione.

In MATLAB questo è disponibile con il comando half per cui una buona parte delle funzioni di default è resa disponibile. Si può interrogare l’inseme delle funzioni disponibili con il comando:

methods(half(1))

che vi restituirà una lista del tipo:

Methods for class half:

abs         asinh       complex     double      floor       int16       islogical   le          logical     mod         plot3       real        scatter3    subsasgn    uint16      ylim        
acos        atan        conj        end         fplot       int32       isnan       length      lt          mrdivide    plotmatrix  rem         sin         subsref     uint32      zlim        
acosh       atanh       cos         eps         ge          int64       isnumeric   line        max         mtimes      plus        reshape     single      sum         uint64      
all         bar         cosh        eq          gt          int8        isreal      log         mean        ndims       pow10       rgbplot     sinh        tan         uint8       
any         barh        cospi       exp         half        isempty     isscalar    log10       min         ne          pow2        round       sinpi       tanh        uminus      
area        ceil        ctranspose  expm1       hypot       isfinite    isvector    log1p       minus       numel       prod        rsqrt       size        times       uplus       
asin        colon       display     fix         imag        isinf       ldivide     log2        mldivide    plot        rdivide     scatter     sqrt        transpose   xlim   

Per estrarre performance dall’utilizzo della precisione half e, più in generale, dall’utilizzo contemporaneo di dati in più precisioni (mixed precision) è necessario avere dell’hardware che possa lavorare in maniera diretta in questo formato, cioè senza adoperare continuamente conversioni o simulare la precisione ridotta. Per le alte performance parliamo di oggetti come le NVIDIA GPUs (CUDA Capabilitiy \(\geq 7.0\)), Google TPUs e diversi tipi di FPGA più o meno sperimentali.

MATLAB ha un supporto limitato (ma in espansione) per lavorare sulle GPU, non esploreremo oltre questa direzione, ma è utile che sappiate che esistono questi possibili sviluppi.

Bibliografia

Hig02

Nicholas J. Higham. Accuracy and stability of numerical algorithms. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, second edition, 2002. ISBN 0-89871-521-0. URL: https://doi.org/10.1137/1.9780898718027, doi:10.1137/1.9780898718027.

Kle06

A. Klein. A generalized Kahan-Babuška-summation-algorithm. Computing, 76(3-4):279–293, 2006. URL: https://doi.org/10.1007/s00607-005-0139-x, doi:10.1007/s00607-005-0139-x.

Neu74

A. Neumaier. Rundungsfehleranalyse einiger Verfahren zur Summation endlicher Summen. Z. Angew. Math. Mech., 54:39–51, 1974. URL: https://doi.org/10.1002/zamm.19740540106, doi:10.1002/zamm.19740540106.

IEEE75419

IEEE-754. IEEE 754-2019, Standard for Floating-Point Arithmetic. IEEE, New York, NY, USA, June 2019. ISBN 1-5044-5925-3 (print), 1-5044-5924-5 (e-PDF). URL: https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=8766229, doi:https://doi.org/10.1109/IEEESTD.2019.876622.