Laboratorio 7b : Il Metodo di Eliminazione di Gauss e la Fattorizzazione LU

Il metodo di eliminazione di Gauss (Carl Friedrich Gauss, 1777-1855), noto anche come algoritmo di riduzione per le righe, è un algoritmo per risolvere sistemi quadrati di equazioni lineari. Come avete visto a lezione si riduce ad una sequenza di operazioni eseguite sulla corrispondente matrice di coefficienti.

Alcune estensioni di questo metodo possono essere utilizzate anche per calcolare il rango di una matrice, il determinante di una matrice quadrata e l`inversa di una matrice invertibile.

Implementare la fattorizzazione LU

Se \(A\) è una matrice \(n\) per \(n\) su un campo \(\mathbb{K}\) (\(A \in M_n(\mathbb{K})\)), allora \(A\) si dice «avere una fattorizzazione \(LU\)» se esiste una matrice triangolare inferiore \(L \in M_n(\mathbb{K})\) e una matrice triangolare superiore \(U \in M_n(\mathbb{K})\) tale che

\[A = LU.\]

Questo è particolarmente utile, poiché, se \(A = LU\), e se \(L\) ed \(U\) sono invertibile, allora ogni soluzione \(\mathbf{y}\) di \(L\mathbf{y} = \mathbf{b}\) produrrà una soluzione \(\mathbf{x}\) di \(A\mathbf{x} = \mathbf{b}\) via \(U\mathbf{x} = \mathbf{y}\).

Pericolo

In generale non tutte le matrici \(A\) ammettono una fattorizzazione \(LU\) di questa forma, si consideri ad esempio la matrice:

\[\begin{split}A = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} l_{11} & 0 \\ l_{12} & l_{22} \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} \\ 0 & u_{22} \end{bmatrix} = LU,\end{split}\]

questa richiederebbe di avere gli elementi diagonali \(u_{ii}\), \(l_{ii}\), \(i=1,2\), diversi da \(0\), ma questo contraddirebbe \(0 = A_{11} = l_{11}u_{11}\).

Una condizione necessaria e sufficiente affinché una fattorizzazione di questa forma esista per una matrice \(A \in M_n(\mathbb{K})\), \(\mathbb{K} = \mathbb{R},\mathbb{C}\), è che

\[\begin{split}\operatorname{rank}(A_{11}) + k \geq \operatorname{rank}([A_{11}\,A_{12}]) + \operatorname{rank}\left(\begin{bmatrix}A_{11}\\A_{21}\end{bmatrix}\right),\end{split}\]

per \(k = 1,\ldots,n-1\) e

\[\begin{split}A = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix}, \qquad A_{11} \in M_k(\mathbb{K}).\end{split}\]

Quando esiste la decomposizione \(LU\) non è unica (le combinazioni di \(L\) e \(U\) per una data \(A\) sono infinite). Per determinare un algoritmo univoco è necessario porre determinati vincoli su \(L\) o \(U\) (Tabella 10).

Varianti dell’algoritmo \(LU\).

Tabella 10 Varianti dell’algoritmo \(LU\).

Nome	Vincoli
Doolittle	\(l_{i,i} = 1\), \(i=1,\ldots,n\)
Crout	\(u_{i,i} = 1\), \(i=1,\ldots,n\)
Choleski	\(U = L^T\)

Come primo esercizio implementeremo la fattorizzazione \(LU\) nella forma di Doolittle, che è quella più strettamente legata all’algoritmo di eleminazione di Gauss che conoscete sin dal corso di algebra lineare.

Se scriviamo l’uguaglianza \(A = LU\) con il vincolo aggiuntivo per cui \(l_{i,i} = 1\), per \(i=1,\ldots,n,\) possiamo ricavare che i termini della matrice \(U\) sono dati da

(9)\[\begin{split}\forall\,j\quad & \begin{array}{ll} i = 1, & u_{i,j} = a_{i,j},\\ i > 1, & u_{i,j} = \displaystyle a_{i,j} - \sum_{k=1}^{i-1} l_{i,k} u_{k,j}, \end{array}\end{split}\]

mentre quelli della matrice \(L\) sono dati da:

(10)\[\begin{split}\forall\,i\quad & \begin{array}{ll} j = 1, & l_{i,j} = \frac{a_{i,j}}{u_{j,j}}, \\ j > 1, & l_{i,j} = \displaystyle \frac{a_{i,j} - \sum_{k=1}^{j-1} l_{i,k} u_{k,j} }{u_{j,j}}. \end{array}\end{split}\]

Esercizio

Si usino le relazioni (9) e (10) per implementare la versione di Doolittle dell’algoritmo \(LU\) per una matrice quadrata. Un prototipo della funzione è dato da:

function [L,U] = doolittlelu(A)
%%DOOLITTLELU Calcola la fattorizzazione LU della matrice A con i vincolo di
%Doolittle.

% Controllo degli input:

% Pre-allocazione memoria:
L = eye(n,n);
U = zeros(n,n);
%!! Questa potrebbe essere anche:
% L = zeros(n,n);
% U = zeros(n,n);
% Dipende da come decidete di utilizzare le formule...

% Utilizzo delle formule per l_{ij} e u_{ij}.

end

• Si faccia un controllo dell’input: la matrice \(A\) è quadrata?

• Si utilizzino operazioni vettorizzate per le somme che compaiono in (9) e (10)

Per verificare la buona riuscita dell’implementazione si può usare il seguente problema di test.

%% Test della versione di Doolittle dell'algoritmo LU  

clear; clc;

A = [ 3 -1  4;
     -2  0  5;
      7  2 -2 ];
[L,U] = doolittlelu(A);
fprintf("|| A - LU || = %1.2e\n",norm(A - L*U,2));

% Vediamone gli ingressi:
format rat
disp(A)
disp(L)
disp(U)
disp(L*U)
format short

Suggerimento

Guardando alla formulazione delle equazioni (9) e (10) potremmo osservare che in realtà possiamo sovrascrivere le entrate della matrice \(A\) con la fattorizzazione \(LU\). Se avete concluso la prima parte pensate a come è possibile realizzare questa versione.

Un suggerimento più estensivo

Possiamo sviluppare il ciclo di istruzioni sostanzialmente in due ordine, in un primo procediamo alla fattorizzazioni colonna per colonna, ovvero:

for k=1:n
    L(k:n,k) = A(k:n,k) / A(k,k); % Dividiamo per il Pivot
    U(k,1:n) = A(k,1:n);          % Aggiorniamo le entrate della U
    A(k+1:n,1:n) = A(k+1:n,1:n) - L(k+1:n,k)*A(k,1:n);
end
U(:,end) = A(:,end);

Nel caso dell”esempio vediamo:

\[\begin{split}k = 0, \qquad L = \left(\begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right) \qquad U = \left(\begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right), \qquad A = \left(\begin{array}{ccc} 3 & -1 & 4\\ -2 & 0 & 5\\ 7 & 2 & -2 \end{array}\right)\end{split}\]

\[\begin{split}k = 1, \qquad L^{(1)} = \left(\begin{array}{ccc} 1 & 0 & 0\\ -\frac{2}{3} & 0 & 0\\ \frac{7}{3} & 0 & 0 \end{array}\right), \qquad \left(\begin{array}{ccc} 3 & -1 & 4\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right) \qquad A^{(1)} = \left(\begin{array}{ccc} 3 & -1 & 4\\ 0 & -\frac{2}{3} & \frac{23}{3}\\ 0 & \frac{13}{3} & -\frac{34}{3} \end{array}\right), \\\end{split}\]

\[\begin{split}k = 2, \qquad L^{(2)} = \left(\begin{array}{ccc} 1 & 0 & 0\\ -\frac{2}{3} & 1 & 0\\ \frac{7}{3} & -\frac{13}{2} & 0 \end{array}\right), \qquad U^{(2)} = \left(\begin{array}{ccc} 3 & -1 & 4\\ 0 & -\frac{2}{3} & \frac{23}{3}\\ 0 & 0 & 0 \end{array}\right), \qquad A^{(2)} = \left(\begin{array}{ccc} 3 & -1 & 4\\ 0 & -\frac{2}{3} & \frac{23}{3}\\ 0 & 0 & \frac{77}{2} \end{array}\right), \\\end{split}\]

\[\begin{split}k = 3, \qquad L^{(3)} = \left(\begin{array}{ccc} 1 & 0 & 0\\ -\frac{2}{3} & 1 & 0\\ \frac{7}{3} & -\frac{13}{2} & 1 \end{array}\right), \qquad U^{(3)} = \left(\begin{array}{ccc} 3 & -1 & 4\\ 0 & -\frac{2}{3} & \frac{23}{3}\\ 0 & 0 & \frac{77}{2} \end{array}\right), \qquad A^{(3)} = \left(\begin{array}{ccc} 3 & -1 & 4\\ 0 & -\frac{2}{3} & \frac{23}{3}\\ 0 & 0 & \frac{77}{2} \end{array}\right)\end{split}\]

La seconda alternativa è quella di eseguire questo ciclo procedendo lungo le righe della matrice

for i = 1:1:n
    for j = 1:(i - 1)
        L(i,j) = (A(i,j) - L(i,1:(j - 1))*U(1:(j - 1),j)) / U(j,j);
    end
    j = i:n;
    U(i,j) = A(i,j) - L(i,1:(i - 1))*U(1:(i - 1),j);
end

Nel caso dell”esempio vediamo:

\[\begin{split}i = 0, \qquad L = \left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right), \qquad U = \left(\begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right), \qquad A = \left(\begin{array}{ccc} 3 & -1 & 4\\ -2 & 0 & 5\\ 7 & 2 & -2 \end{array}\right),\end{split}\]

\[\begin{split}i = 1, \qquad L^{(1)} = \left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right), \qquad U^{(1)} = \left(\begin{array}{ccc} 3 & -1 & 4\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right),\end{split}\]

\[\begin{split}i = 2, \qquad L^{(2)} = \left(\begin{array}{ccc} 1 & 0 & 0\\ -\frac{2}{3} & 1 & 0\\ 0 & 0 & 1 \end{array}\right), \qquad U^{(2)} = \left(\begin{array}{ccc} 3 & -1 & 4\\ 0 & -\frac{2}{3} & \frac{23}{3}\\ 0 & 0 & 0 \end{array}\right)',\end{split}\]

\[\begin{split}i = 3, \qquad L^{(3)} = \left(\begin{array}{ccc} 1 & 0 & 0\\ -\frac{2}{3} & 1 & 0\\ \frac{7}{3} & -\frac{13}{2} & 1 \end{array}\right), \qquad U^{(3)} = \left(\begin{array}{ccc} 3 & -1 & 4\\ 0 & -\frac{2}{3} & \frac{23}{3}\\ 0 & 0 & \frac{77}{2} \end{array}\right)',\end{split}\]

L”unica differenza tra le due implementazioni è l’ordine, per colonna e per riga rispettivamente, in cui facciamo le operazioni.

La fattorizzazione con pivoting

Per fare sì che la fattorizzazione \(LU\) si possa calcolare per una generica matrice (ovvero anche quando si incontrano pivot nulli) e per migliorare la stabilità dell’algoritmo , possiamo introdurre una strategia di scambio delle righe della matrice detta, per l’appunto, di pivoting parziale.

Formalmente, questo vuol dire che otterremo una fattorizzazione della forma

\[P A = L U,\]

in cui \(P\) è una matrice di permutazione. Strutturalmente una matrice di permutazione non è nient’altro che una matrice identità di cui abbiamo permutato le righe. Vediamo un veloce esempio:

format rat
H = hilb(5)
P = eye(5)
P = P([5:-1:1],:)
P*H

che costruisce le matrici

\[\begin{split}H = \left(\begin{array}{ccccc} 1 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5}\\ \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6}\\ \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7}\\ \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8}\\ \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} & \frac{1}{9} \end{array}\right), \quad P = \left(\begin{array}{ccccc} 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 \end{array}\right), \quad PH = \left(\begin{array}{ccccc} \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} & \frac{1}{9}\\ \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8}\\ \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7}\\ \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6}\\ 1 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} \end{array}\right),\end{split}\]

e ci mostra anche come possiamo permutare due (o più) righe di una matrice MATLAB. Abbiamo ora tutti gli ingredienti necessari a costruire la nostra versione fatta in casa della fattorizzazione LU con pivoting in MATLAB.

Esercizio

Si costruisca una funzione ludecomp per costruire la fattorizzazione \(LU\) con pivoting parziale per una matrice \(A\). Un prototipo della funzione è quindi:

function [L,U,P] = ludecomp(A)
%%LUDECOMPP Fattorizzazione LU con pivoting parziale.

% Controllo dell'input:

% Allocazione della memoria:
L = zeros(n);
U = zeros(n);
P = eye(n);

% Fattorizzazione con Pivoting
end

• Si faccia un controllo dell’input: la matrice \(A\) è quadrata?

• Si utilizzino operazioni vettorizzate per le somme che compaiono in (9) e (10).

Suggerimento

Se il ciclo esterno è per \(k=1,\ldots,n\) possiamo individuare il pivot facendo:

[~,r] = max(abs(A(k:end,k)));
r = n-(n-k+1)+r; % Trasliamo l'indice in questione

Qual è l’effetto della traslazione di indice?

Possiamo verificare l’implementazione della versione con pivoting parziale facendone un paragone con la versione dell’esercizio precedente.

Confrontiamo gli errori assoluti e relativi,

\[E_{\text{abs}} = \| A - LU\|_2, \qquad E_{\text{rel}} = \frac{\| A - LU\|_2}{\| A\|_2},\]

tra la matrice \(A\) ed il prodotto dei termini \(LU\) ottenuti con i diversi algoritmi (con e senza pivoting parziale).

clear; clc; close all;
sizes = 100:100:1500;
N = length(sizes);
maxerr = zeros(N,1);
relerr = zeros(N,1);
maxerrm = zeros(N,1);
relerrm = zeros(N,1);
for i = 1:N
   A = rand(sizes(i),sizes(i));
   [L,U] = doolittlelu(A);
   [Lm,Um,P] = ludecomp(A);
   normA = norm(A,2);
   maxerr(i) = norm(A - L*U,2);
   relerr(i) = maxerr(i)/normA;
   maxerrm(i) = norm(P*A - Lm*Um,2);
   relerrm(i) = maxerrm(i)/normA;
   fprintf("Dimensione %d\n \t || A - LU || = %1.2e\n",sizes(i),maxerr(i));
   fprintf("\t || A - LU ||/||A|| = %1.2e\n",relerr(i));
   fprintf("\t || P*A - LU ||/||A|| = %1.2e\n",maxerrm(i));
   fprintf("\t || P*A - LU ||/||A|| = %1.2e\n",relerrm(i));
end

figure(2)
loglog(sizes,maxerr,'o-',sizes,relerr,'x-',...
    sizes,maxerrm,'o-',sizes,relerrm,'x-','LineWidth',2);
xlabel('Dimensione');
legend({'Errore Assoluto','Errore Relativo',...
    'Errore Assoluto (Pivoting)','Errore Relativo (Pivoting)'},...
    'Location','best','FontSize',14);

Quello che osserviamo nella figura è una crescita di più di un’ordine di grandezza dell’errore assoluto nella fattorizzazione \(LU\) senza pivoting, ed un certo numero di oscillazioni Fig. 6.

Ci aspetteremmo che almeno l”errore relativo si comportasse meglio. Quello che sta accadendo è che la scelta dei pivot affidata alla forma originale della matrice sta introducendo dell’instabilità numerica che ci fa perdere in precisione relativa più di quanto sarebbe lecito aspettarsi guardando ai numeri di condizionamento delle operazioni in questione.

L’implementazione con pivoting, invece, permette di mantenere un errore relativo che è all’incirca della precisione di macchina, migliorando sensibilmente le performance rispetto alla versione che utilizzava l’ordinamento di partenza.

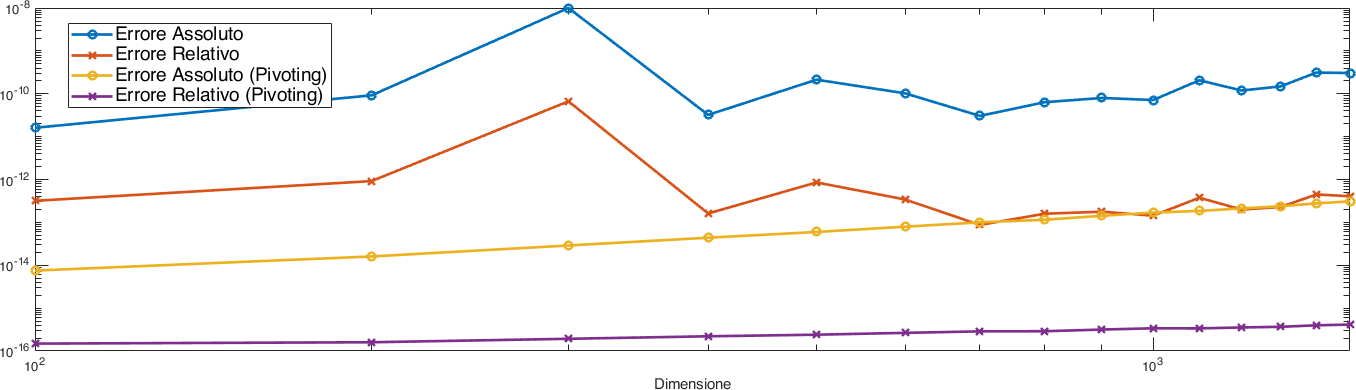
Fig. 6 Errori assoluti e relativi tra una matrice \(A\) ad entrate casuali uniformemente distribuite in \([0,1]\) e la relativa fattorizzazione \(LU\) calcolata senza e con pivoting.

Calcolo del determinante

Dopo aver calcolato la fattorizzazione \(LU\) di una matrice \(A\) è possibile utilizzarla anche per calcolare il determinante della matrice \(A\). Si può fare sfruttando il teorema di Binet che ricordiamo collega il prodotto fra matrici quadrate con il determinante:

\[\det(AB) = \det(A)\det(B), \qquad \forall\,A,B \in M_n(\mathbb{K}),\]

ed, in particolare,

\[\det(A) = \det(LU) = \det(L)\det(U),\]

che, se usiamo la formulazione di Doolittle si riduce quindi ad essere:

\[\det(A) = \det(LU) = \det(L)\det(U) = \prod_{i=1}^{n} l_{ii} \prod_{i=1}^n u_{ii} = 1 \prod_{i=1}^n u_{ii} = \prod_{i=1}^n u_{ii}.\]

Che possiamo riportare facilmente su MATLAB come:

function res = ludet(A)
%%LUDET Calcola il determinante della matrice A sfruttando la sua fattorizzazione
%LU in forma di Doolittle e senza pivoting.
[~,U] = doolittlelu(A);
res = prod(diag(U));
end

e testare rapidamente con:

A = pascal(5,2);
fprintf('Errore relativo: %1.2e\n',abs(ludet(A) - det(A))/abs(det(A)));

che ci dovrebbe restituire un errore relativo, rispetto alla funzione det nativa di MATLAB dell’ordine di 3.33e-16.

Avvertimento

Per costruire il calcolo del determinante anche nel caso in cui si utilizzi la fattorizzazione \(LU\) con pivoting è necessario tenere traccia del numero di scambi di righe effettuati.

Le funzioni di MATLAB

MATLAB ha implementata tra le sue routine una versione della fattorizzazione \(LU\) ed un algoritmo per la soluzione dei sistemi lineari.

Per la fattorizzazione LU il comando ha il medesimo nome lu e permette una certa flessibilità.

• [L,U] = lu(A), restituisce una matrice triangolare superiore in \(U\) e una matrice triangolare inferiore permutata in \(L\), tale che \(A = LU\). La matrice di input \(A\) può essere densa o sparsa.

• [L,U,P] = lu(A), restituisce una matrice triangolare inferiore \(L\) con diagonale di uno, matrice triangolare superiore \(U\) ed una matrice di permutazione \(P\) tale che \(PA = LU.\) Con un argomento di input opzionale è possibile scegliere il formato della \(P\), ovvero se chiama lu(A, outputForm) con outputForm uguale a 'matrix' (default) \(P\) è memorizzata come una matrice, se si chiama con l’opzione 'vector' allora \(P\) è un vettore tale che A(P,:) = L*U.

• [L,U,P,Q] = lu(A) restituisce una matrice triangolare inferiore \(L\) con diagonale di uno, matrice triangolare superiore \(U\) e due matrici di permutazione \(P\) e \(Q\) tali che \(PAQ = LU\). Per una matrice sparsa questa opzione è significativamente più efficiente della versione con tre output.

Definition 1

Una matrice sparsa o array sparso è una matrice in cui la maggior parte degli elementi è zero. Per dare una definizione rigorosa riguardo alla proporzione di elementi di valore zero affinché una matrice sia qualificata come sparsa è tipicamente necessario considerare la sorgente del problema che la ha generata, e.g., la discretizzazione di una PDE. Un criterio comune è che il numero di elementi diversi da zero sia approssimativamente uguale al numero di righe o colonne.

Al contrario, se la maggior parte degli elementi è diversa da zero, la matrice è considerata densa.

Informazioni sulle matrici sparse possono essere recuperate dal manuale di MATLAB (help sparse). Non scenderemo qui in ulteriori dettagli.

La funzione per risolvere i sistemi lineari è la funzione mldivide \. Si tratta di una delle funzioni più elaborate di MATLAB, il comando A\B è la divisione matriciale di A in B, moralmente è la stessa operazione di INV(A)*B, ma è calcolata in modo diverso, stabile ed efficiente.

Se \(A\) è una matrice \(N\) per \(N\) e \(\mathbf{b}\) è un vettore colonna con \(N\) componenti, o una matrice con più di queste colonne, allora X = A\b è la soluzione dell’equazione A*X = B.

Avvertimento

Viene stampato un messaggio di avviso se A è scalata male o malcondizionata, ad esempio

x = hilb(15)\ones(15,1);

restituisce

Warning: Matrix is close to singular or badly scaled. Results may be inaccurate.
RCOND =  5.460912e-19.

Esercizi

Consideriamo alcune applicazioni ingegneristiche del problema calcolare le soluzione di un sistema [Kiu15].

Esercizio

La formulazione per gli spostamenti di una trave reticolare piana è simile a quella di un sistema di masse e molle. Le differenze sono che

1. i termini di rigidità sono dati da \(k_{i} = (E A/L)_ {i}\), dove \(E\) è il modulo di elasticità, \(A\) rappresenta l’area della sezione di taglio e \(L\) è la lunghezza dell’elemento;

2. ci sono due componenti dello scostamento in ogni punto di giuntura.

Per la trave reticolare in figura:

Fig. 7 Profilo di un elemento della trave reticolare piana.

si ottiene quindi il seguente sistema di equazioni lineari

\[K \mathbf{u} = \mathbf{p}\]

dove

K = [27.58  7.004 -7.004 0 0
     7.004 29.57  -5.253 0 -24.32
    -7.004 -5.253 29.57  0 0
    0 0 0 27.58 -7.004
    0 -24.32 0 -7.004 29.57];
p = [0 0 0 0 -45]'; % kN

si determinino tutti gli scostamenti \(u_i\) per il sistema.

Esercizio

Riprendiamo l’esperimento fatto ne La fattorizzazione con pivoting con la matrice di Hilbert

\[(H_n)_{i,j} = \int_{0}^{1} x^{i+j-2}\,{\rm d}x = \frac{1}{i+j-1}, \qquad i,j=1,\ldots,n\]

che è un noto esempio di matrice malcondizionata. Si scriva un programma specializzato nella risoluzione delle equazioni \(H \mathbf{x} = \mathbf{b}\) mediante il metodo di decomposizione \(LU\) con e senza pivoting, dove \(H\) è la matrice di Hilbert di dimensione arbitraria \(n \times n\), e

\[b_i = \sum_{j=1}^{n} (H_n)_{i,j},\]

L’unico input del programma deve essere \(n\). Eseguendo il programma, si determinino i più grandi valori di \(n\) per i due algoritmi per cui la soluzione è entro 6 cifre significative della soluzione esatta.

Sistema di molle

Fig. 8 Sistema lineare di molle.

Esercizio

Il sistema mostrato in Fig. 8 è costituito da \(n\) molle lineari che supportano \(n\) masse. Le costanti elastiche delle molle sono indicate con \(k_i\), i pesi delle masse sono \(W_i\), e \(x_i\) sono gli spostamenti delle masse (misurati dalle posizioni in cui le molle sono indeformate). La cosiddetta formulazione dello spostamento si ottiene scrivendo l’equazione di equilibrio di ciascuna massa e sostituendo le forze elastiche con \(F_i = k_i (x_{i+1} - x_{i} )\).

Il risultato è il sistema simmetrico e tridiagonale di equazioni

\[\begin{split}\begin{split} (k_1 + k_2) x_1 - k_2 x_2 = & W_1,\\ - k_i x_{i-1} + (k_i + k_{i+1}) x_i - k_{i+1} x_{i+1} = & W_i, \qquad i=2,3,\ldots,n-1,\\ -k_n x_{n-1} + k_n x_n = & W_n, \end{split}\end{split}\]

si scriva un programma che risolve queste equazioni per dati valori di \(n\), \(\mathbf{k}\) e \(\mathbf{W}\). Si risolva il problema con \(n=5\) e

\[\begin{split}\begin{split} k_1 = k_2 = k_3 = 10\, \text{N}/\text{mm}\;\; k_4 = k_5 = 5\, \text{N}/\text{mm}\\ W_1 = W_3 = W_5 = 100\,\text{N},\qquad W_2 = W_4 = 50\,\text{N}. \end{split}\end{split}\]

Bibliografia

Kiu15

Jaan Kiusalaas. Numerical Methods in Engineering with MATLAB®. Cambridge University Press, 3 edition, 2015. doi:10.1017/CBO9781316341599.